搓OS-day6

手搓OS-day6

区分子序列与子串：子序列是可以剔除部分中间不相等的部分，而子串必须是连续的。

这个问题是不能采用暴力遍历的，因为时间复杂度高的可怕，要采用动态规划的方法，而动态规划的最重要的就是找到状态转移函数

现有两个序列X[]和Y[]，长度分别为m和n，lcs()函数为求最长公共子序列长度的函数。

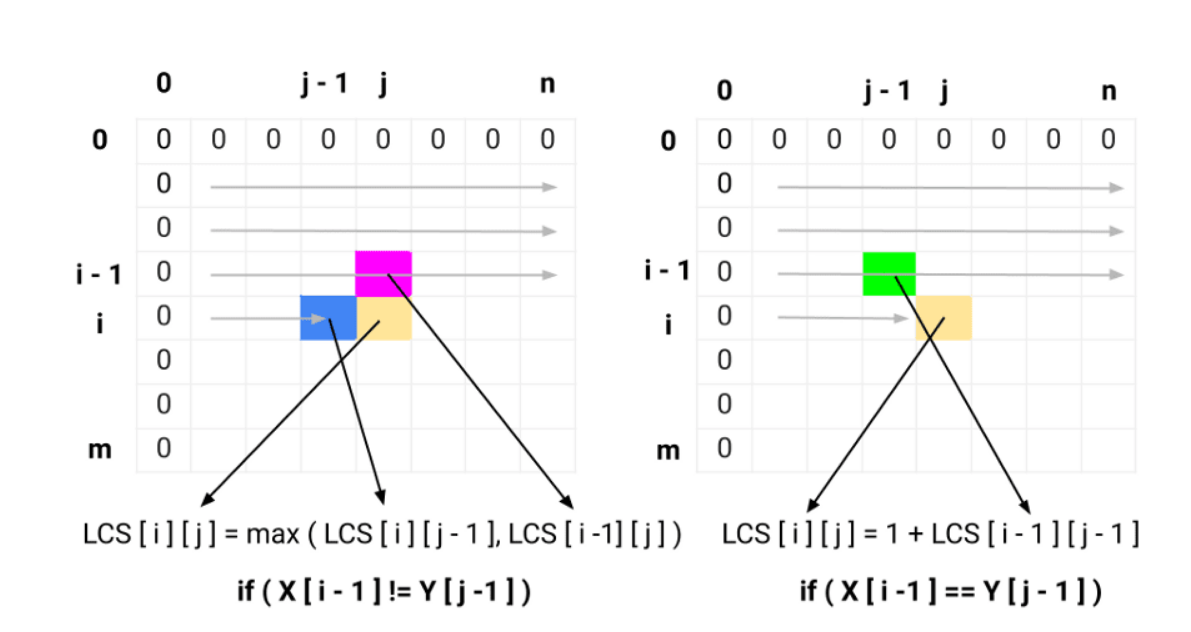
性质1：如果串的最后一个元素相同，例如：if (X[m-1]==Y[n-1])，那么其最长子序列长度，则在剩余的m-1与n-1个元素的最长子序列加一，公式表现为：

1	if(X[m-1]==Y[n-1]) lcs(X,Y,m,n)=lcs(X,Y,m-1,n-1)+1;

性质2：如果串的最后一个元素不相同，例如，if(X[m-1]!=Y[n-1])，则取下面两种情况的最大值：

从公式上表达为：

1 2	if(X[m-1]!=Y[n-1]) lcs(X,Y,m,n)=max(lcs(X,Y,m-1,n),lcs(X,Y,m,n-1));

递归方法能发现其计算了一些重复值，于是考虑通过动态规划的方式来存储已经计算过的结果，下面是其表中作业的形式：

实际上，上面表的生成是可以看做一个有向无环图，每一个数的生成都依赖一个或两个数，于是我们从表的右下角起步，对其进行某种拓扑排序，就能得到一个LCS序列

老师的网站上的图不是非常清晰，但是第一个网站里的一张图并结合上面的依赖，会非常清晰：

如果建立在动态规划上，每一条计算的分支都是可以并行的，那么我们就可以开始尝试了，下面还有一个升级版的并行方案，在最后一个链接，菜，实现了一个非常简单的并行（甚至可能不如单独算快），核心要点是要保护对角上的元素的访问，这个对角比较广义，核心的一条代码就是这样子的：

1
2
3

spin_lock(&result_lock);
result = MAX(result, dp[N - 1][M - 1]);
spin_unlock(&result_lock);

给我小小的编程经历带来了大大的并行震撼，还得补一下高性能计算（哎，又是坑）