图神经网络——GNN初步

最简单的图神经网络——着眼于节点

这张图就挺清楚了，但是我们还有一些问题没有说清楚，数据是什么，数据在哪儿，数据怎么运算，目的是什么

从派别上，更像是频率派，实际上是在分析各个节点之间的一个关系。

target：节点嵌入(隐)状态（\(h_v\)）

数学表达：

节点邻居：

点集：\(co[v]\)
边集：\(ne[v]\)

节点嵌入：\(x_v\)

输出嵌入：\(o_v\)

局部转移函数： \[ h_v=f(x_v,x_{co[v]},h_{ne[v]},x_{ne[v]}) \] 局部输出函数： \[ o_v=g(h_v,x_v) \] 学习方法：梯度下降 \[ loss=\sum_{i=1}^{p}{(t_i-o_i)} \] p是所有的目标节点的数目

缺点

缺点实际上是相当显然的

缺乏对边的学习
传递效率低
梯度消失
多次迭代后点的值是固定的、平滑的，fixed node，导致整个图的区分意义不大

GCN——着眼全图

傅里叶变换

通俗来讲，我们平时见到的连续可导函数，都是建立在时域，傅里叶变换就要要将他变换到频域

那么频域又是什么东西？

频域首先要有频率，那么是什么出现的频率，比如是周期函数才有频率，最经典的周期函数正是三角函数，傅里叶很开创的搞出来了所有的函数都可以用三角函数来分解的一个变换，就是傅里叶变换。

空间域：空域，又称图像空间，说白了就是像素级处理。

图谱理论

拉普拉斯算子

一个多元函数的所有二阶偏导数 \[ \Delta f=\sum^{n}_{i}{\frac{\part^2 f }{\part x_i^2}} \] 考虑一个二元函数\(f(x,y)\)，则拉普拉斯算子可以表示为： \[ \Delta f=\frac{\part^2f}{\part x^2}+\frac{\part^2f}{\part y^2} \] 可以从单侧差分公式中有： \[ \Delta f \approx \frac{f(x+\Delta x,y)+f(x-\Delta x,y)-2f(x,y)}{(\Delta x)^2}+\frac{f(x,y+\Delta y)+f(x,y-\Delta y)-2f(x,y)}{(\Delta y)^2} \] 对二元函数离散化采样： \[ \begin{bmatrix} f(x_1,y_1)&f(x_2,y_1) &\cdot\cdot\cdot & f(x_n,y_1)\\ f(x_1,y_2)& f(x_2,y_2) &\cdot\cdot\cdot &f(x_n,y_2) \\ \cdot\cdot\cdot &\cdot\cdot\cdot &\cdot\cdot\cdot &\cdot\cdot\cdot \\ f(x_1,y_n)& f(x_2,y_n) &\cdot\cdot\cdot &f(x_n,y_n) \end{bmatrix} \] 令\(\Delta x=x_{i+1}-x_i=1,\Delta y=y_{i+1}-y_i=1\)

则点\((x_i,y_i)\)的laplace算子可以如下公式近似计算： \[ \frac{f(x_i+\Delta x,y_i)+f(x_i-\Delta x,y_j)-2f(x_i,y_j)}{(\Delta x)^2}+\frac{f(x_i,y_j+\Delta y)+f(x_i,y_j-\Delta y)-2f(x_i,y_j)}{(\Delta y)^2} \]

\[ =\frac{f(x_{i+1},y_j)+f(x_{i-1},y_j)-2f(x_i,y_j)}{1^2}+\frac{f(x_i,y_{j+1})+f(x_i,y_{j-1})-2f(x_i,y_j)}{1^2} \]

\[ =f(x_{i+1},y_j)+f(x_{i-1},y_j)+f(x_i,y_{j+1})+f(x_i,y_{j-1})-4f(x_i,y_j) \]

于是他就变成了一个离散的一个中心和四个相邻节点的图的结构，将laplace算子离散化表示： \[ \Delta f=\sum_{(k,l)\in N(i,j)}^{}{(f(x_k,y_l)-f(x_i,y_j))} \] 很惊喜的发现，卷积出现了！

谱聚类方法推导和对拉普拉斯矩阵的理解 - 知乎 (zhihu.com)

laplace 矩阵

有无向图\(G=（E,V）\),\(V\)有n个节点，邻接矩阵为W，加权度矩阵D，将lapace算子扩展到图上： \[ \Delta f_i=\sum_{j \in N_i}{w_{ij}(f_i-f_j)} \] 那么我们可以改写成矩阵形式： \[ \Delta f=\begin{bmatrix} \Delta f_1 \\ \cdot \cdot \cdot \\ \Delta f_n \\ \end{bmatrix}=\begin{bmatrix} d_1f_1-w_1f \\ \cdot \cdot \cdot \\ d_nf_n-w_nf\\ \end{bmatrix}=\begin{bmatrix} d_1 && && \\ && \cdot \cdot \cdot&&\\ && &&d_n\\ \end{bmatrix}\begin{bmatrix} f1 \\ \cdot \cdot \cdot \\ f2\\ \end{bmatrix}-\begin{bmatrix} w_1\\ \cdot \cdot \cdot \\ w_2\\ \end{bmatrix} \begin{bmatrix} f_1\\ \cdot \cdot \cdot \\ f_2\\ \end{bmatrix} \]

\[ =\mathbf{(D-W)f} \]

那么就有laplace矩阵 \[ \mathbf{L}=\mathbf{D-W} \] 性质：

对任意向量\(f \in \mathbb{R^n}\)，有\(\mathbf{f^T Lf}=\frac{1}{2}\sum_{i=1}^{n}{\sum_{j=1}^{n}{w_{ij}(f_i-f_j)^2}}\)
laplace矩阵时半正定矩阵
laplace矩阵的最小特征值为0，其对应的特征向量常向量1，级所有分量为1
laplace矩阵有n个非负实数特征值。

归一化laplace矩阵

对称归一化： \[ L=D^{-1/2}LD^{-1/2}=I-D^{-1/2}WD^{-1/2} \] 随机漫步归一化： \[ L_{rw}=D^{-1}L=I-D^{-1}W \]

谱网络到GCN

谱网络通过对归一化laplace进行特征分解在频域上建立了卷积核： \[ g_{\theta} *x=Ug_{\theta}(\Lambda) U^Tx \] 其中\(U\)是对称归一化的laplace矩阵进行特征值分解后的特征向量，\(\Lambda\)是相对应的特征值

很显然此运算极其复杂，包括一个很大的矩阵函数，而且卷积核规模受限，因此引入了多项式进行逼近截断： \[ g_{\theta}(\Lambda)\approx \sum_{k=0}^{K}{\theta_k \Lambda^k} \] ChebNet引入了切比雪夫多项式 \(T_k\)对 \(g_\theta\) 进行拟合。切比雪夫多项式有个重要性质: \[ T_n(cos(\theta))=cos(n\theta) \]

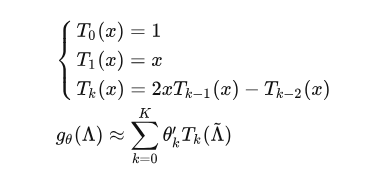
\(\tilde{\Lambda}=2\frac{\Lambda}{\lambda_{max}}-I\)，那么卷积核就转化为： \[ g_{\theta} *x=\sum_{k=0}^{K}{\theta_K^`UT_{k}(\tilde \Lambda) U^Tx} \] 令K=1，则 \[ g_{\theta} *x=\sum_{k=0}^{1}{\theta_K^`UT_{k}(\tilde \Lambda) U^Tx}=\theta_0x+\theta_1(\frac{2}{\lambda_{max}}L-I_N)x \] 由于正则化后的拉普拉斯矩阵特征值最大不超过2，令\(\lambda_{max}=2\) \[ g_{\theta} *x=\theta_0x+\theta_1(\frac{2}{\lambda_{max}}L-I_N)x =\theta_0x+\theta_1(L-I_N)x \] 又因为： \[ L=D^{-1/2}LD^{-1/2}=I-D^{-1/2}WD^{-1/2} \] 因此： \[ g_{\theta} *x=\theta_0x-\theta_1D^{-1/2}WD^{-1/2}x \] 令\(\theta=\theta_0=-\theta_1\)，共享参数得： \[ g_{\theta} *x\approx\theta(I_N-D^{-1/2}WD^{-1/2})x=\theta(D^{-1/2}\tilde WD^{-1/2})x \] 堆叠卷积层，并进行重整化（或者叫重正则化）： \[ H^{(l+1)}=\sigma(\mathbf{\tilde {D}^{-1/2}\tilde {A}\tilde {D}^{-1/2}H^{(l)}W^{(l)} }) \]

over

空间方法

neural FPS

\[ x=h_v^{t-1}+\sum_{i=1}^{|N_v|}{h_i^{t-1}} \\ h_v^t=\sigma(xW_t^{|N_v|}) \]

还是简单介绍一下，h是节点嵌入或者叫隐层状态，w是某个节点有多少个邻居的权重

PATCHY-SAN

节点序列选择
选择邻居节点作为感受野，共选择k个
图标准化，为感受野节点排序，映射到向量空间
采用CNN架构进行卷积运算

DCNN

扩散卷积神经网络，用于节点分类： \[ \mathbf{H}=\sigma(\mathbf{W^c} \odot P*X) \]

DGCN

dual graph convolutional network（DGCN），

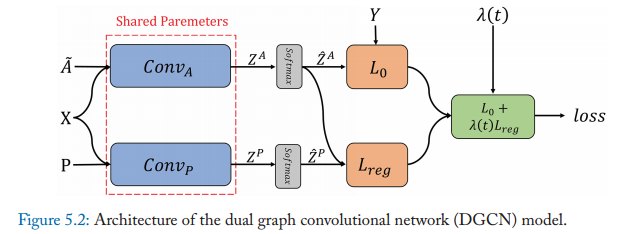
网络架构如上，上面一层采用了最基本的GCN来做运算，在下一层用PPMI矩阵P代替正则化邻接矩阵。其目的是为了统合局部一致性和全局一致性。

PMI是一种来衡量两种事物之间相似性的指标： \[ PMI(x,y)=ln\frac{p(xy)}{p(x)p(y)} \] 令不相关和负相关的PMI值都为0，即得矩阵\(P\)

这是一个很巧妙的构思，实际上将其转变成了一个很经典的loss函数，可以应用各种正则化技巧。

LGCN

learnable graph convolution networks

这个网络是基于可学习网络卷积层和子图训练策略

可学习网络卷积层，利用CNN作为聚合器，通过邻接矩阵获得前k个特征元素，然后利用一维CNN计算隐层： \[ \hat{H}_t=g(H_t,A,k)\\ H_{t+1}=c(\hat{H}_t) \] 其中\(g(\cdot)\)函数为获取特征元素

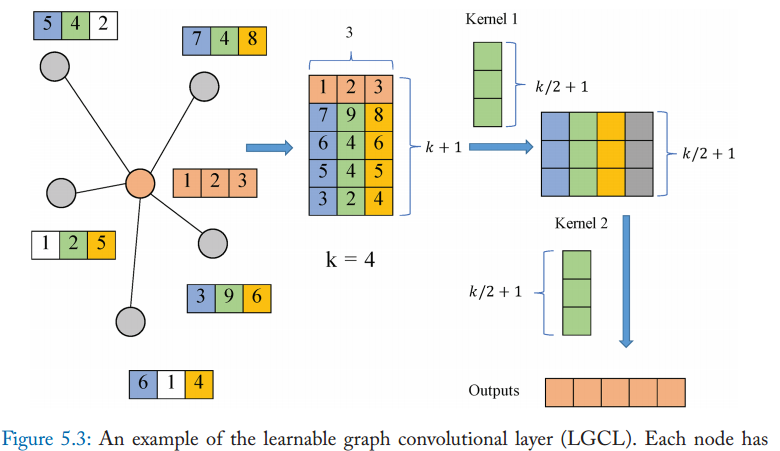
挑战：

如果从股票价格入手，难以构造一个图，其次如何构造一个动态的图，如何有GNN来学习这个动态的图，都很具有挑战性