机器学习作业
作业九 反向传播算法（BP）
算法推导
令input layer 到hidden layer的权重为\(w_{ih}\)，hidden layer和output layer的权重为\(w_{ho}\)
前向算法伪代码：
| Algorithm1: forward |
|---|
| input: X |
| output: \(y\) |
| 1. hidden_in=\(w_{ih}X+b_1\)
2. hidden_out=\(\sigma(hidden\_in)\) 3. output_in=\(w_{ho}X+b_2\) 4. output_out=\(\sigma(output\_out)\) #根据情况可有可无，无的话则output_in即为output_out 5. y=output_out 6. 7. return \(y\) |
output的输出结果为：\(y_j\)，目标结果为\(t_j\)
令误差函数为\(E=\frac{1}{2}\sum_{j=0}^{n}{(y_j-t_j)^2}\)，其中\(i\)为output layer的神经元个数
下面给出反向传播的伪代码：
| Algorithm1: backprop |
|---|
| input: X,t,y,learn_rate |
| output: null |
| 1. \(\delta_1=(y-t)\sigma^{'}(y)\) #output
layer的梯度 2. \(\delta_2=\sigma^{'}(hidden\_output)\sum_{i=0}^{n}{w_{ho}\delta_1}\) #求解hidden layer的梯度 3. 4. \(w_{ih}-=learn\_rate*\delta_2\) 5. \(w_{ho}-=learn\_rate*\delta_1\) 6. \(b_{2}-=learn\_rate*\delta_2\) 7. \(b_{1}-=learn\_rate*\delta_1\) 8. 9. return |
其中梯度求导原因如下： \[ \begin{array}{left} \frac{\partial E}{\partial w_{ij}}=\frac{\partial E}{\partial a{j}}\frac{\partial a_j}{\partial w_{ij}} \\ 其中：\\ E=\frac{1}{2}\sum_{j=0}^{n}{(y_j-t_j)^2}\\ a_j=\sum_i{w_{ij}z_i}\\ z_j=\sigma(a_j)\\ 那么：\\ \frac{\partial E}{\partial a{j}}=y_j-t_j \\ \delta \equiv\frac{\partial E}{\partial a{j}}\\ 则：\\ \frac{\partial E}{\partial w_{ij}}=\delta\frac{\partial a_j}{\partial w_{ij}}=\delta\sigma^{'}(a_j) \end{array} \]
拟合sin曲线
在实现中，output layer输出时不能采用Sigmoid函数激活，否则无法出现正常结果：
1 | import numpy as np |
经过200次迭代后，结果如下：
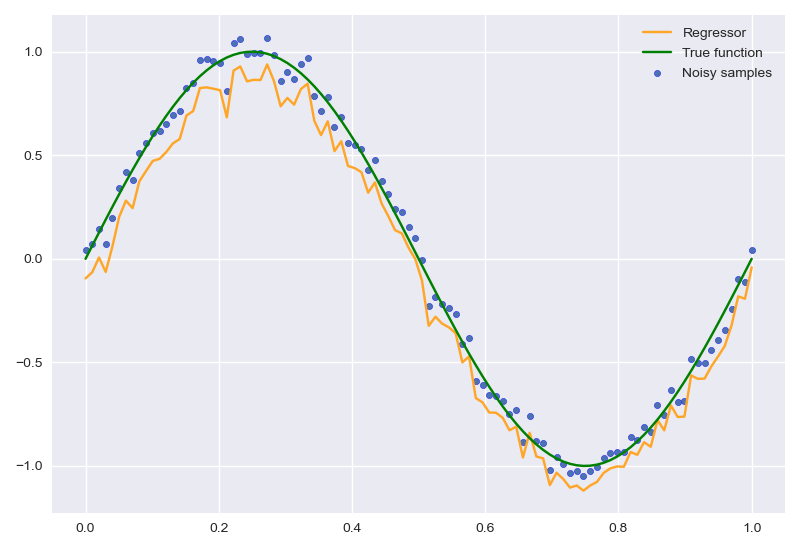
loss曲线如下：
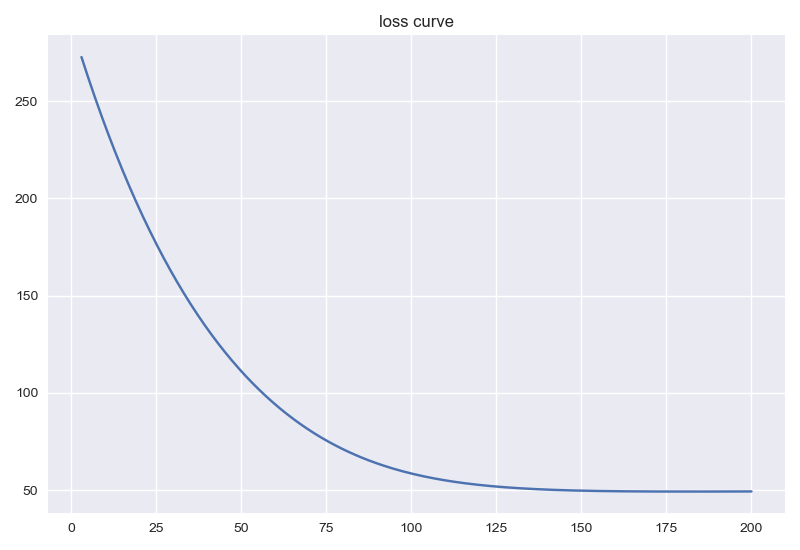
如果迭代2000次：
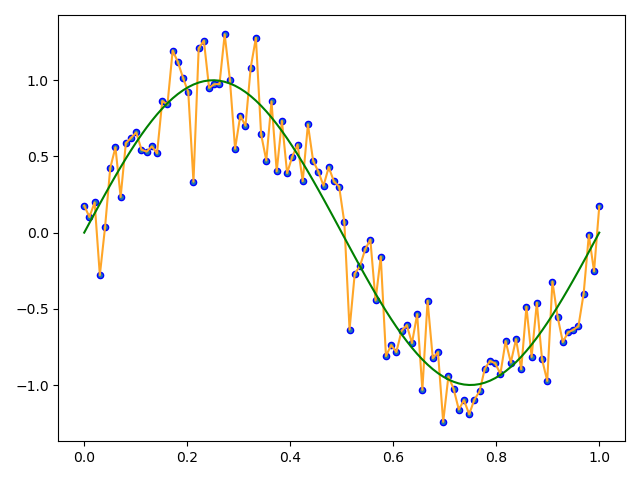
可以看到有明显过拟合。
如果输出结果，采用Sigmoid函数处理：
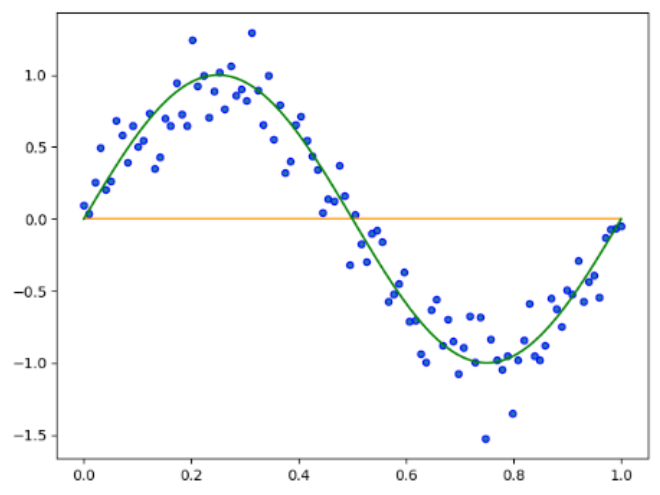
原因很简单，因为Sigmoid函数将数值缩放到了0，导致结果均为0，如果将误差符号反向，那么将得到一条y=1的直线作业八 神经网络初步
作业八 神经网络初步
sklearn中人工神经网络（ANN）主要提供的是多层感知机（MLP），其中有回归和分类两种，回归感知机还有能够自动实现交叉验证的版本。
MLPClassifier二分类
流程如下：
- 导入iris数据，取后两类
- 标准化
- PCA得到x_pca，y
- 初始化MLP，训练
- 绘制分类面
代码如下：
1 | from sklearn.neural_network import MLPClassifier |
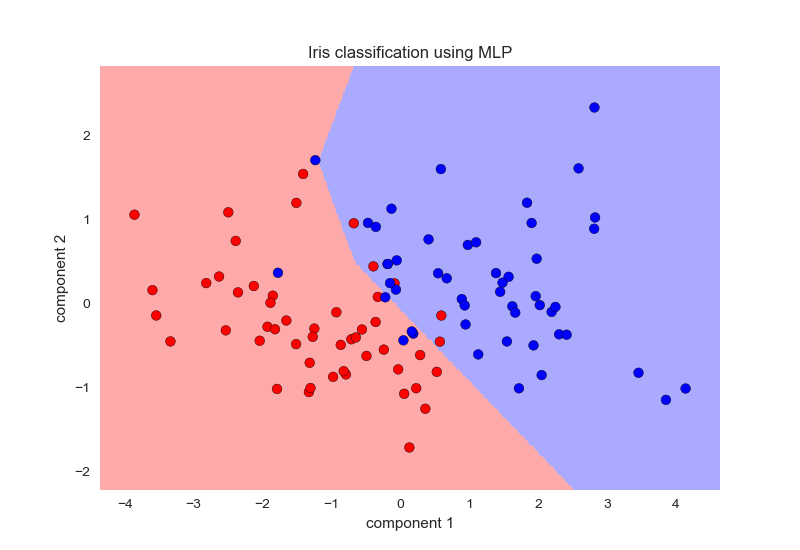
MLPClassifier多分类
流程如下：
- 导入iris数据
- 标准化
- PCA得到x_pca，y
- 初始化MLP，训练
- 绘制分类面
1 | import numpy as np |
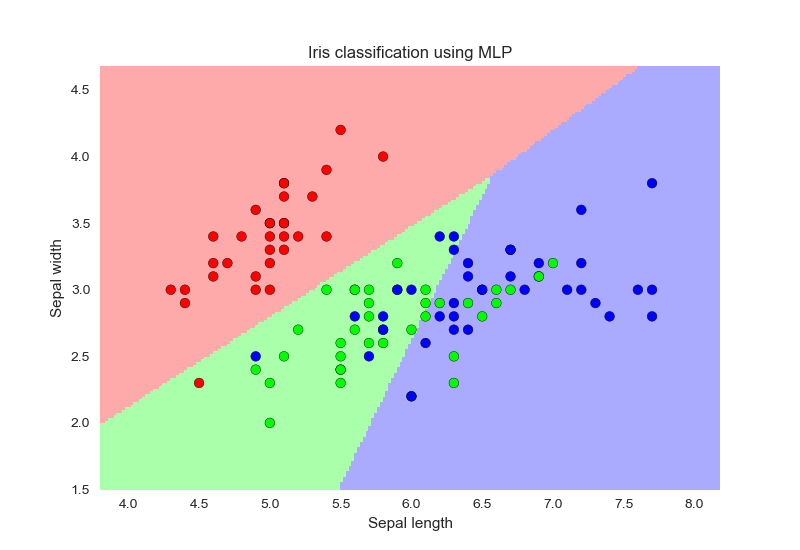
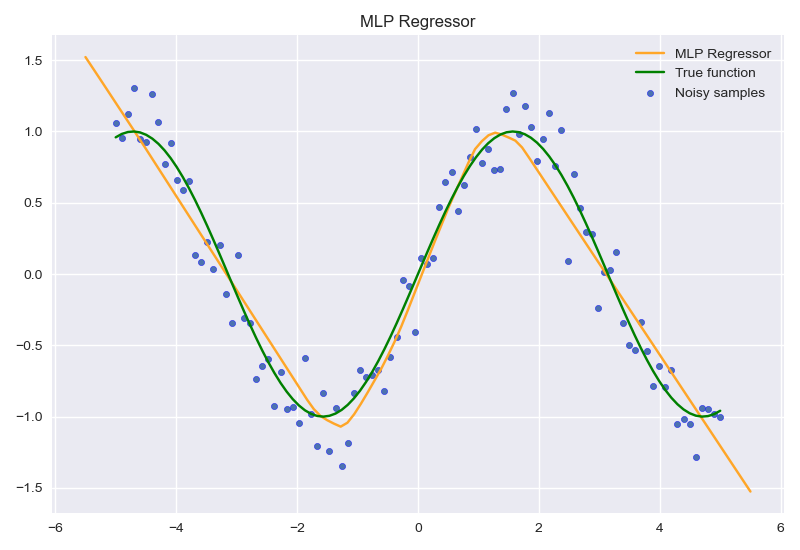
MLPRegressor
程序流程如下：
- 创建数据X，y
- 为y添加随机噪声
- 初始化MLP
- 训练MLP
- 绘制预测效果图
代码如下：
1 | import numpy as np |
作业七 逻辑回归分类
由于都是从sklearn中调用，并不涉及什么复杂算法，因此下面采用列表的方式描述程序作用
二分类逻辑回归
首先说明下面程序的目的：
| 1.观察不同惩罚项系数对应参数变化 |
|---|
| 2.观察不同惩罚项系数对应错误率 |
| 3.可视化二分类结果 |
流程如下：
- 导入iris数据，取后两类
- 标准化
- PCA得到x_pca，y
- 初始化逻辑回归
- 调整参数c，分别训练逻辑回归得到权重参数和错误率
- 绘制错误率和权重参数曲线
- 绘制分类面
代码如下：
1 | from sklearn import datasets |
结果如下：
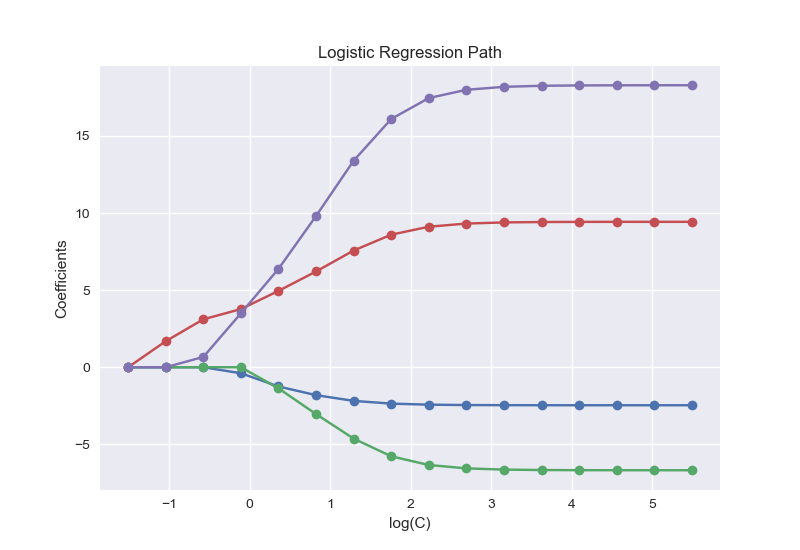
不同惩罚项对应的参数变化，可以看出当惩罚项小于1时，对于模型的稀疏化效果较好。
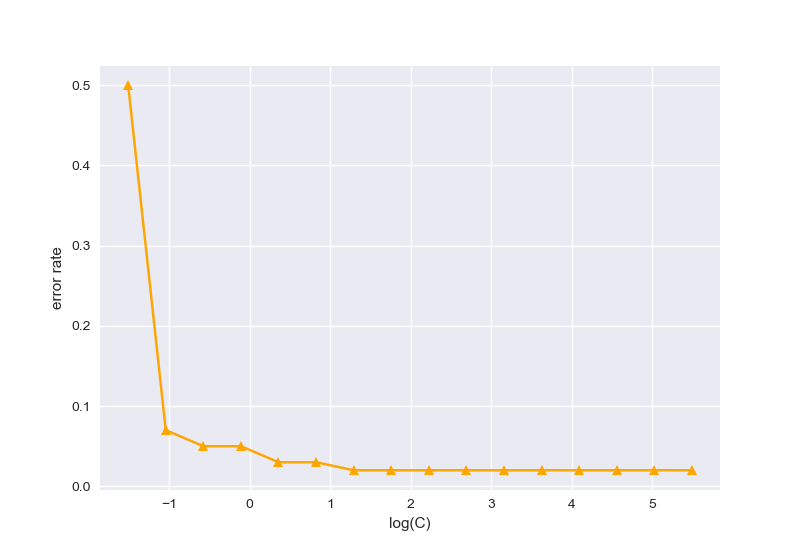
不同惩罚项系数对应的分类错误率，选择为10时效果较好；
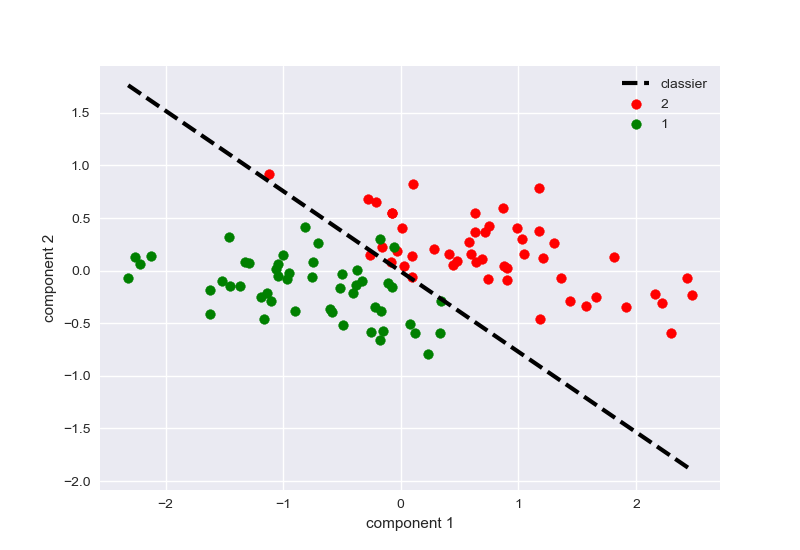
分类结果效果如图：
多分类逻辑回归
首先说明下面程序的目的：
| 1.绘制多分类的分类面 |
|---|
流程如下：
- 导入iris数据
- 标准化
- PCA得到x_pca，y
- 初始化逻辑回归，训练逻辑回归
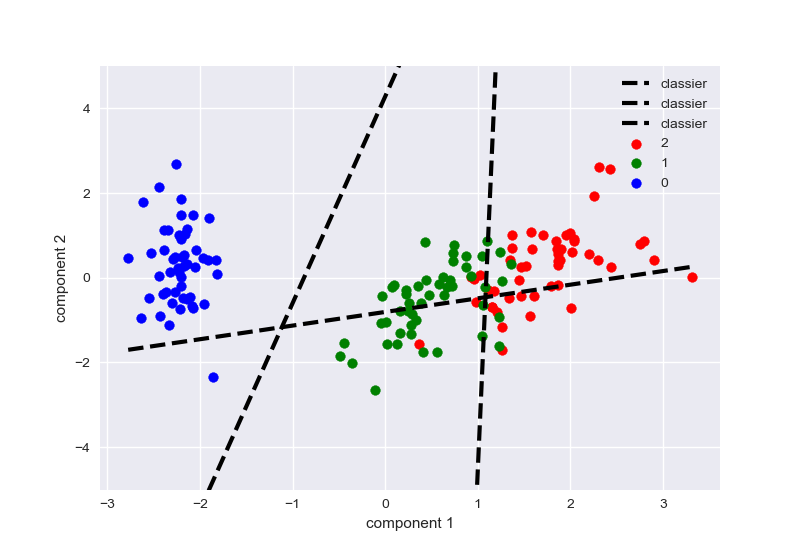
- 绘制分类面
1 | from sklearn import datasets |
作业六
Bayesian Linear Regression
所有算法都放在同一个Python文件下，函数算法伪代码如下：
| Algorithm1: fit |
|---|
| input: X,t,degree, \(\alpha,\beta,\phi\) |
| output: \(m_n,S_n\) |
| 1. \(if\)
len(X.shape) == 1: # 预先判断形状 2. X=X.reshape(-1,1) 3. \(if\) len(t.shape) ==1: 4. t=t.reshape(-1,1) 5. \(S_n^{-1}=\alpha I+\beta\phi(X)^T\phi(X)\) # 计算协方差的逆 6. \(S_n=\)np.linalg.inv(\(S_n^{-1}\)) 7. \(m_n=\beta S_n \phi(X)^Tt\) # 计算均值 8. 9. return \(m_n,S_n\) |
| Algorithm2: predict |
|---|
| input: X, \(\phi,m_n,S_n\) |
| output: \(mean,\sigma^2\) |
| 1. \(\sigma^2\) = \(\frac{1}{\beta}+\phi(X)S_n\phi(X)^T\) 2. mean=\(\phi(x)m_n\) 3. 4. return mean, \(\sigma ^2\) |
代码实现：
1 | import numpy as np |
回归效果：
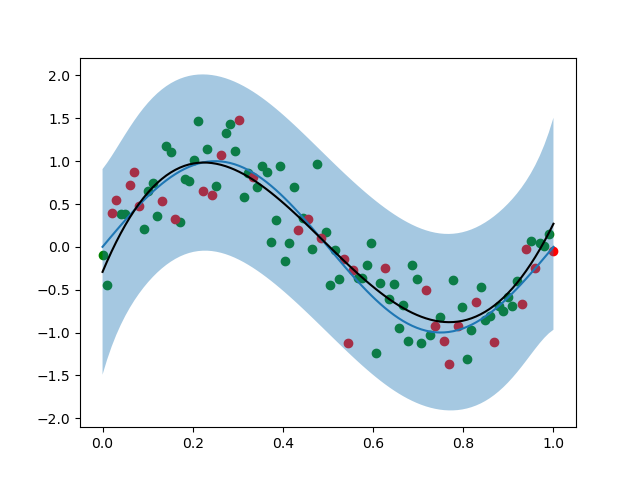
不同样本数量影响拟合效果
1 | x_1=np.linspace(0,1,100) |
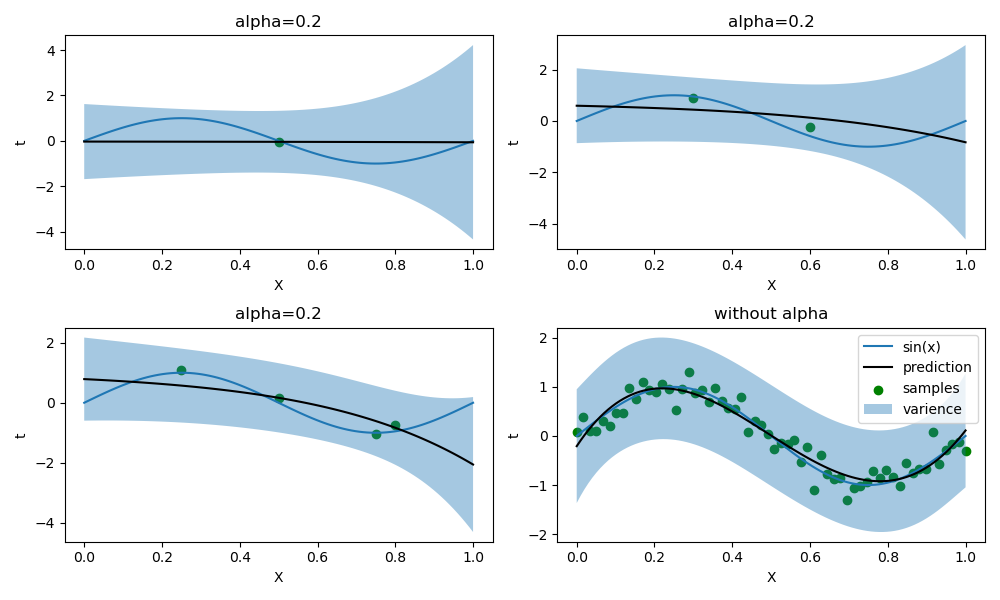
同时，我调整了样本数量较小时的\(\alpha\)值，下图是无正则化的情况（样本数量为1时，必须有正则化否则出现奇异矩阵）：
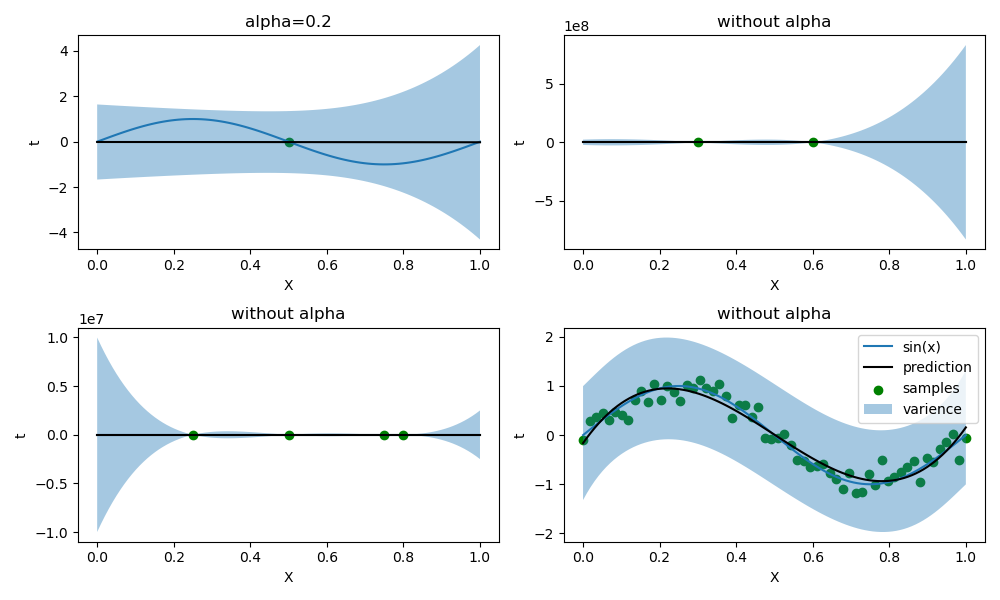
交叉验证调优
因为要做调优，所以固定生成数据，设定种子为0。
在固定\(\alpha=0,beta=10\)时，首先确定degree：
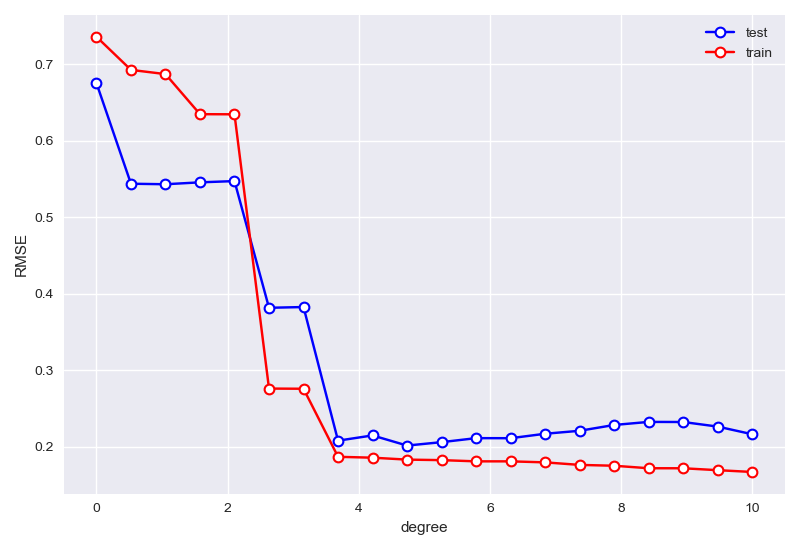
best degree is 9 min RMSE in test sets: 0.2014522467351943
接下来在\(degrer=9\)的情况下，寻找\(\alpha\)的参数最优情况：
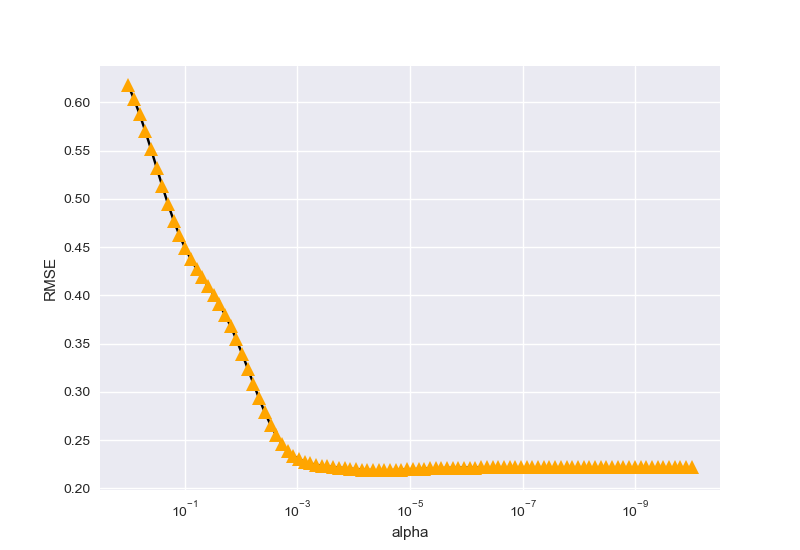
parameter_best is 2.848035868435799e-05
最后，按以上两种情况搜寻参数\(\beta\)：
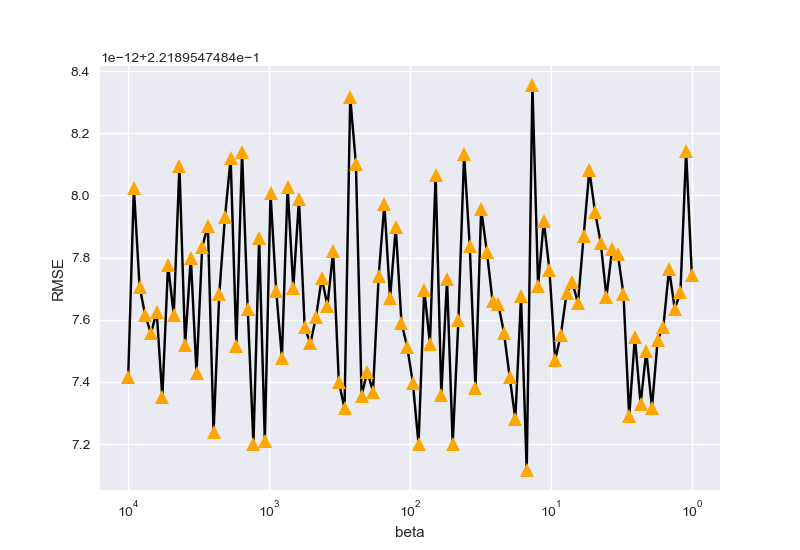
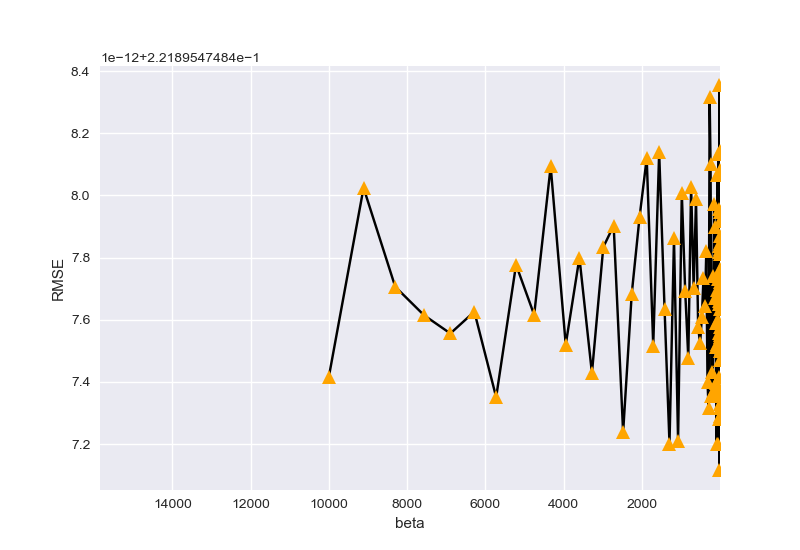
beta_best is 14.84968262254465
最终参数选择结果为：
| \(\alpha\) | 2.848035868435799e-05 |
|---|---|
| \(degree\) | 9 |
| \(\beta\) | 14.84968262254465 |
最终拟合结果：
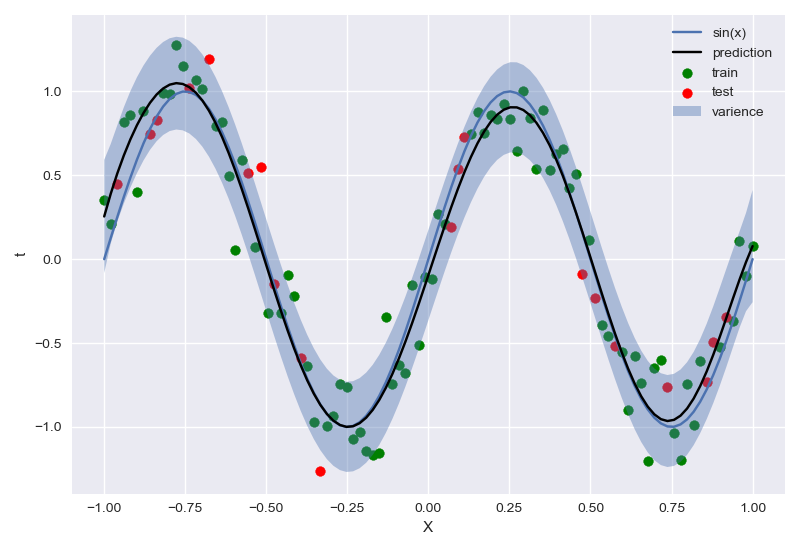
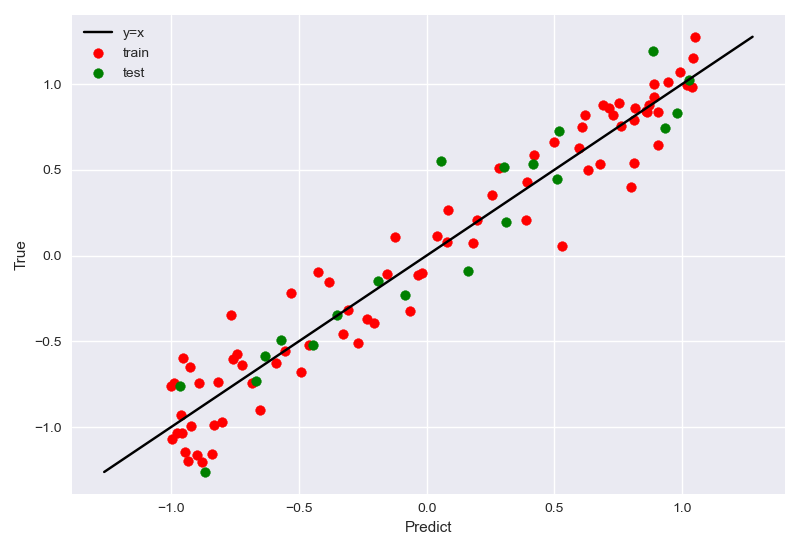
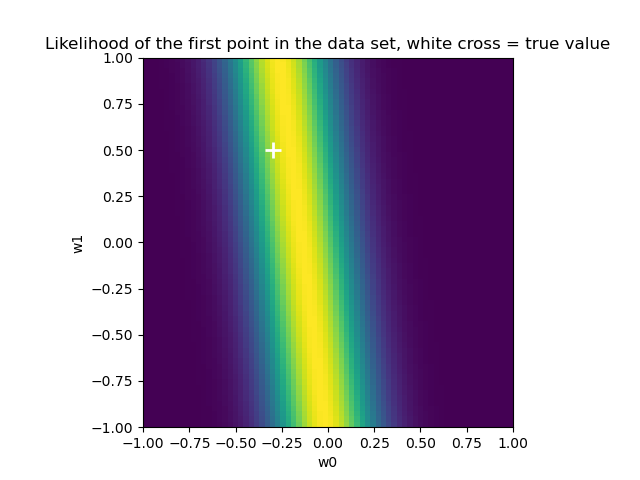
模拟拟合过程（似然、先验）
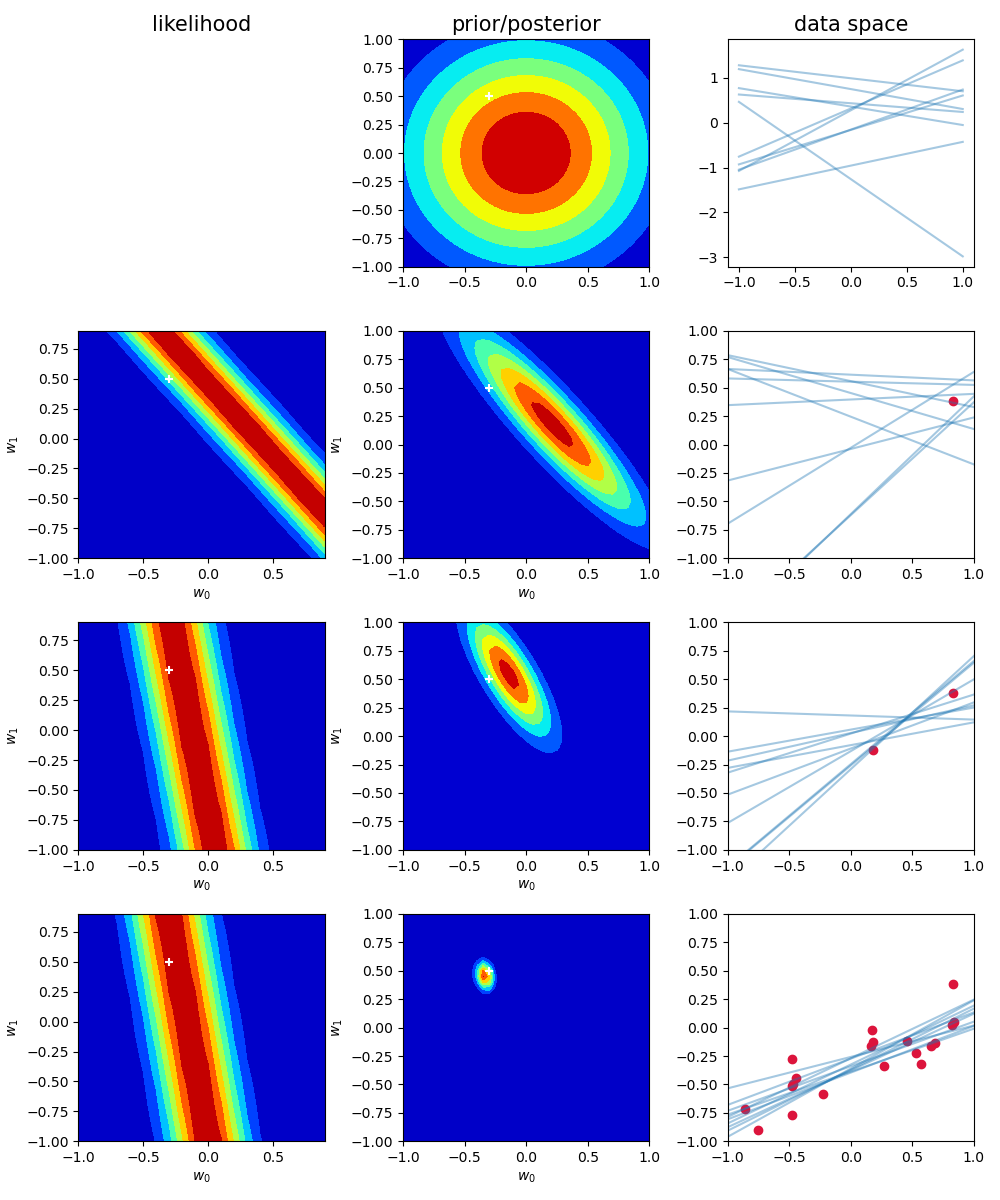
1 | import numpy as np |
作业五
等价核绘制
首先是高斯核的绘制，下图是一个取值为线性的高斯核函数的图像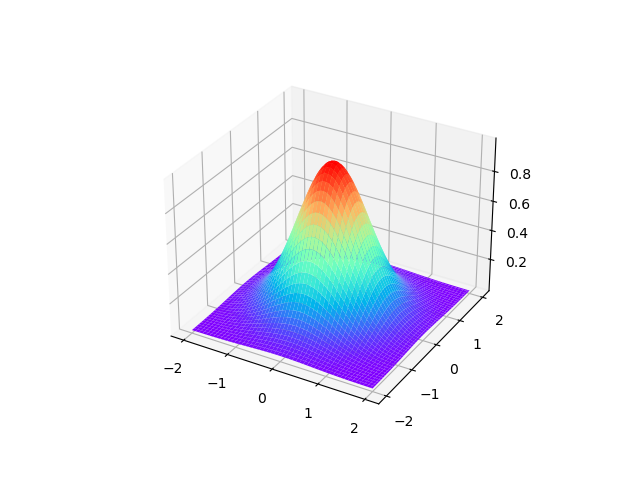
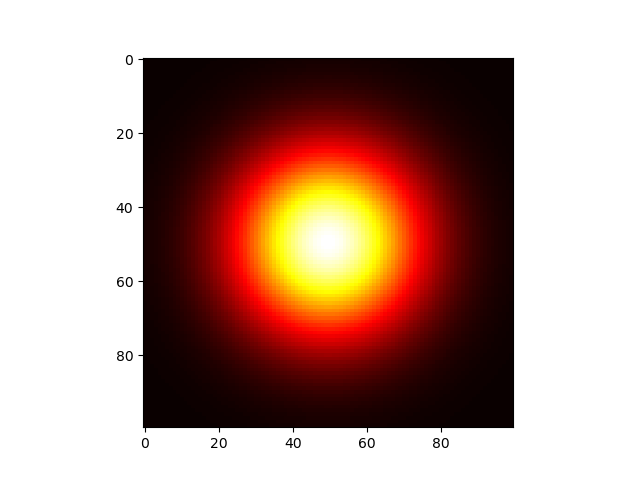
1 | import matplotlib.pyplot as plt |
下面复现课本的等价核：
高斯核
1 | import numpy as np |
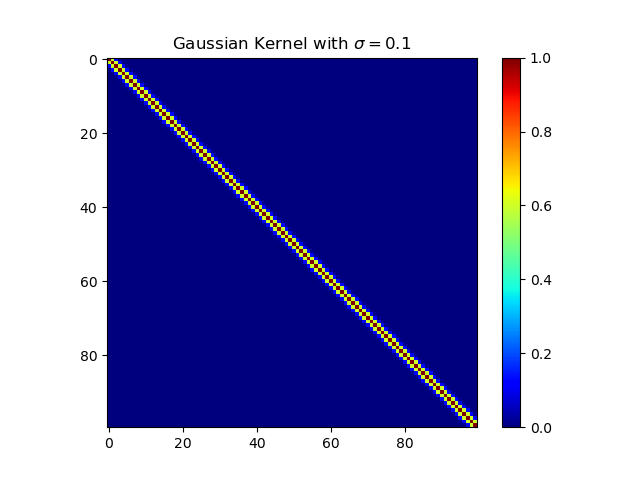
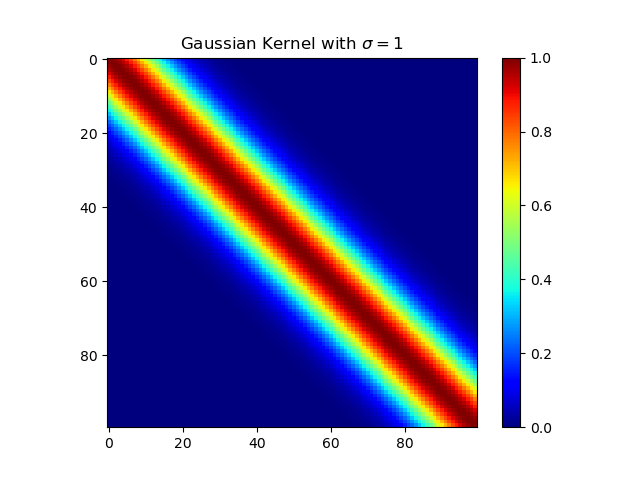
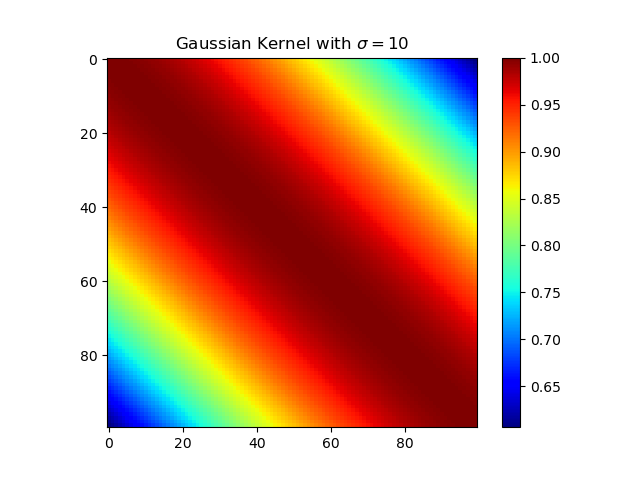
多项式核
1 | import numpy as np |
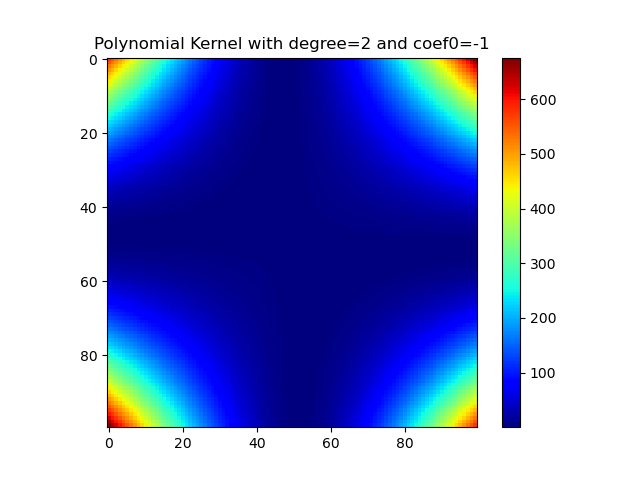
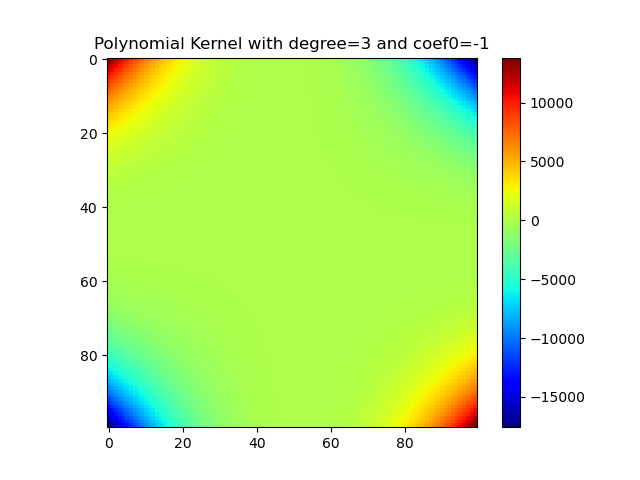
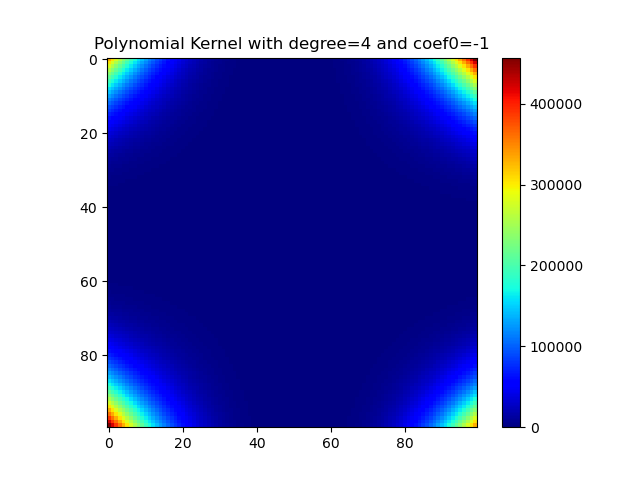
Sigmoid核
1 | import numpy as np |
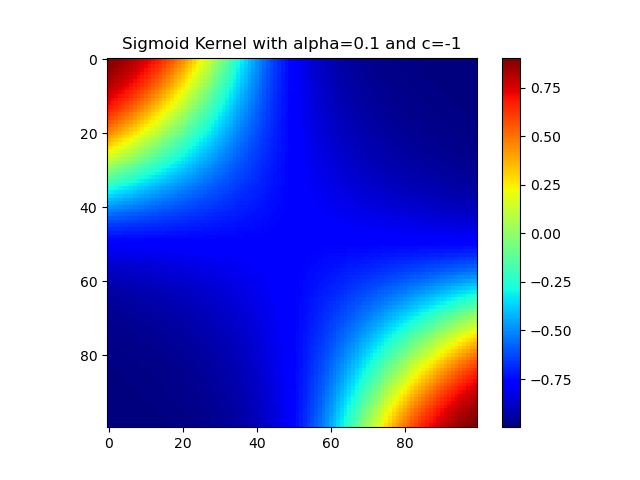
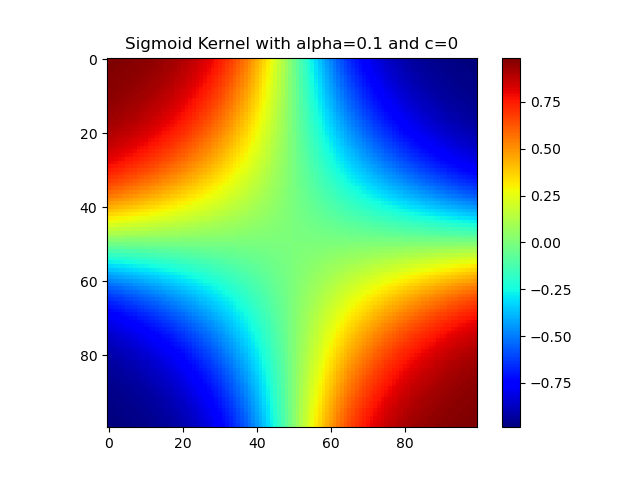
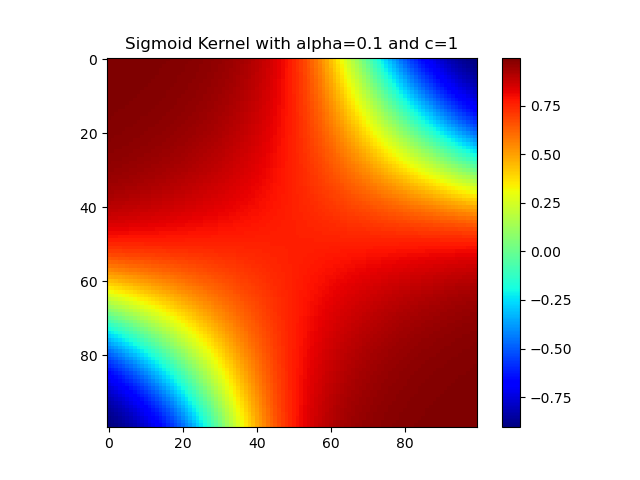
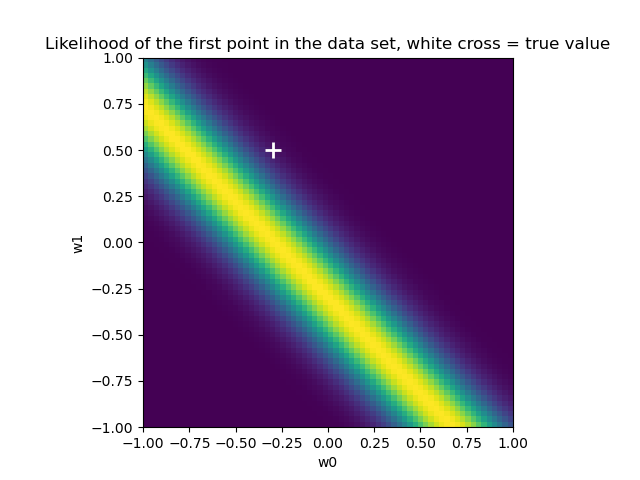
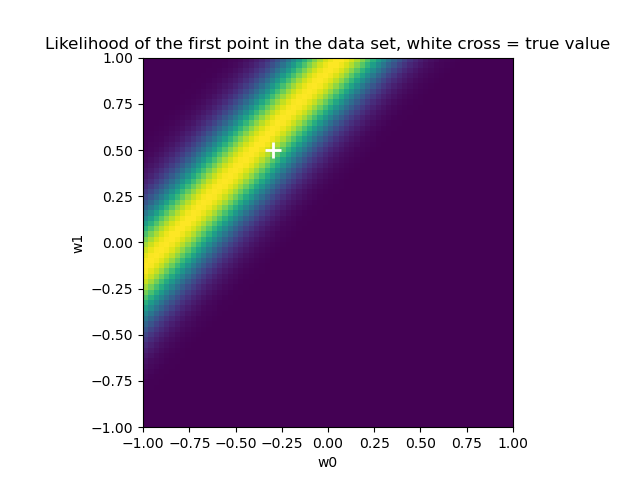
似然
1 | from scipy import stats |
作业一 多项式拟合
理论推导
\[ \min ||f(\omega;x)-t||^2\\ \sum_{i=0}^{n}{\omega_i*x_i^j}=t \]
写成矩阵形式： \[ XW=T \] 使用平方和最小来衡量，设损失函数： \[ L(x)=\frac{1}{2}\sum^{N}_{i=1}{(\sum_{j=0}^{M}{\omega_jx_i^j-y_i)^2}} \] 对损失函数求导，令导数等于0： \[ \begin{array}{l} \frac{\partial L(x;\omega)}{\partial \omega_i}=0 \\ \\ \frac{1}{2}\sum_{i=1}^{N}{2(\sum^{j=0}_{M}{\omega_jx_i^j-y_i)}\times x_i^k}=0 \\ \\ \sum_{i=1}^{N}{\sum^{M}_{j=1}{\omega_ix_i^{j+k}}}=\sum_{j=1}^{M}{x_i^ky_i}(k=0,1,2,3,\cdots,M) \end{array} \] 那么就有： \[ \begin{array}{l} X=\sum^M_{j=1}{x_i^{j+k}} \\ W=\omega_i \\ Y=\sum_{i=1}^{M}{x_i^ky_i}\\ XW=Y \end{array} \] 将以\(x\)为参数的非线性模型转化为以\(w\)的线性模型，从而转化为矩阵方程求解问题,需要将方程特征进行组合，实现上使用sklearn，进行多项式特征组合，然后使用线性回归进行预测：
算法语言描述：
生成一个（特征数目+1，特征数目+1）的矩阵
分别计算0-特征阶数的幂
返回特征混合矩阵
线性回归
代码实现
1 | import numpy as np |
1 | import numpy as np |
1 | import math |
结果对比
不同的特征数量，首先全部针对样本数量为10的情况：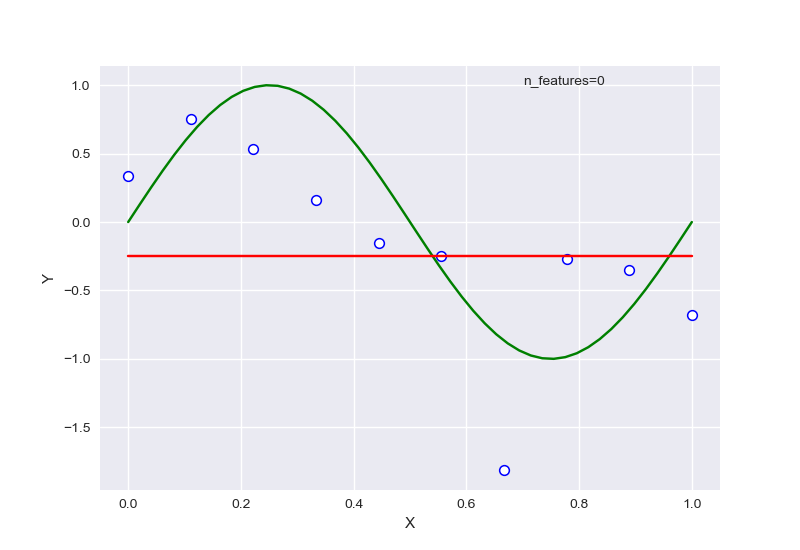 
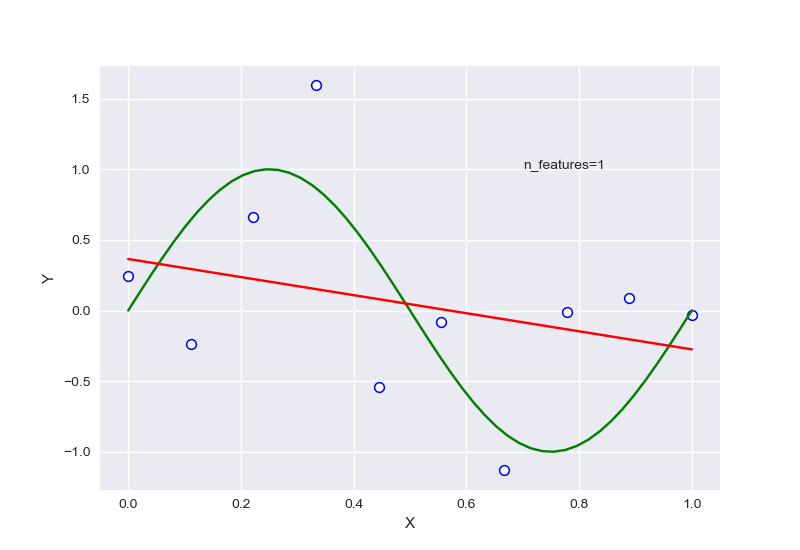
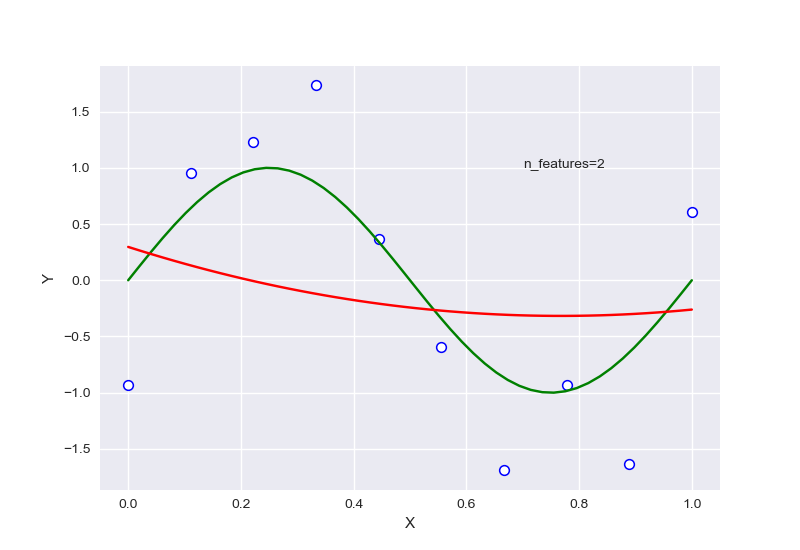
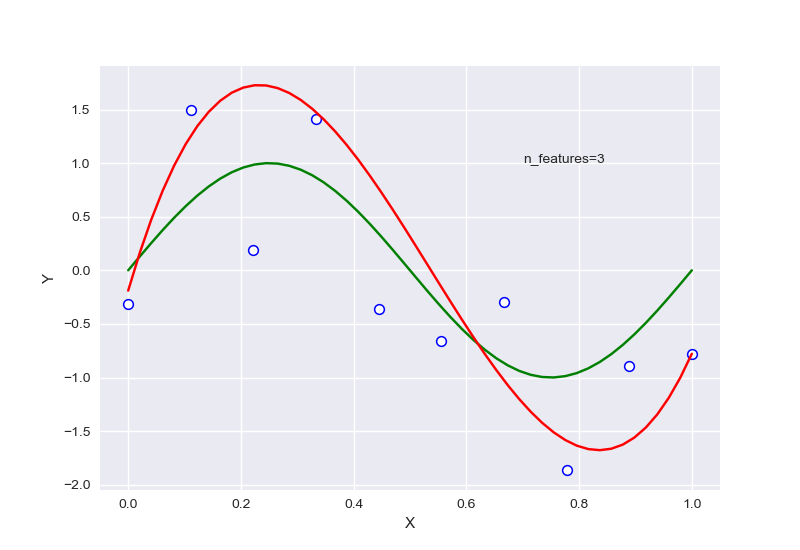
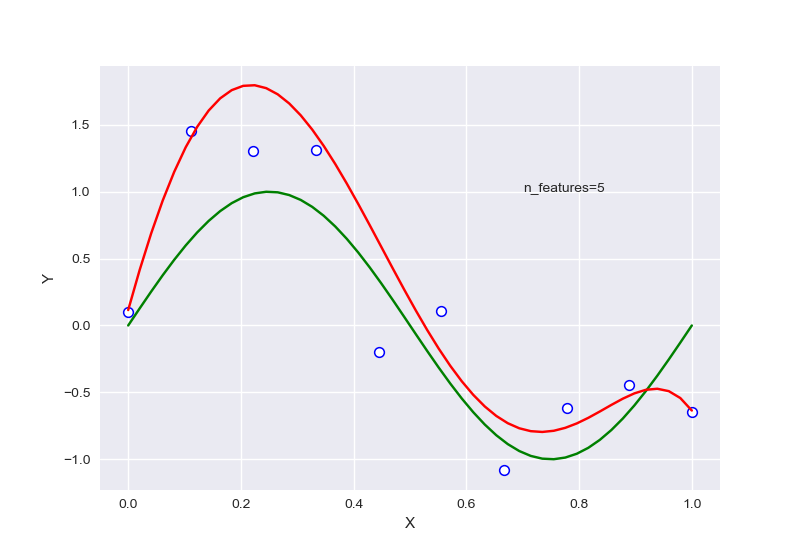
从中可以大致看出，在选择特征过少时，会出现欠拟合现象，选择过多后则会过拟合，针对样本量为20的情况下，RSME曲线如图：
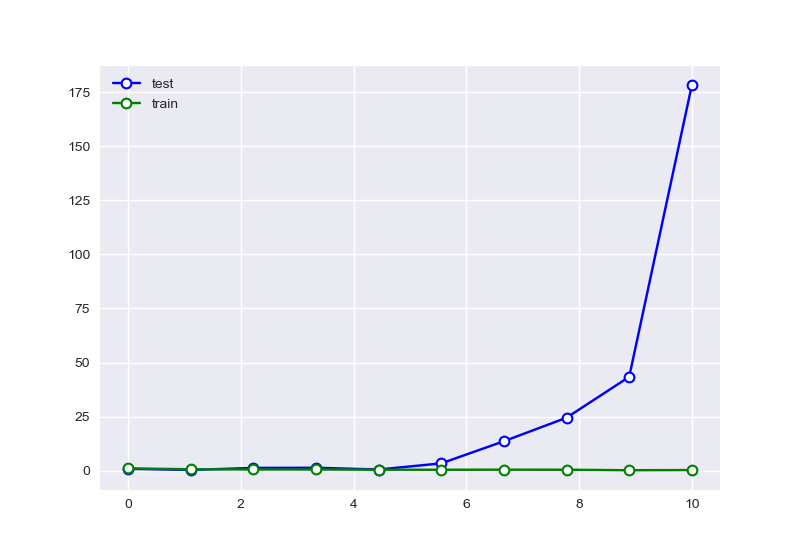图上显示的情况，并不是与我们预期中的情况完全吻合，其原因可能是因为测试集样本数量过少，导致无法很好的捕捉曲线拟合的问题，于是我们对其他样本数量进行对比
、 
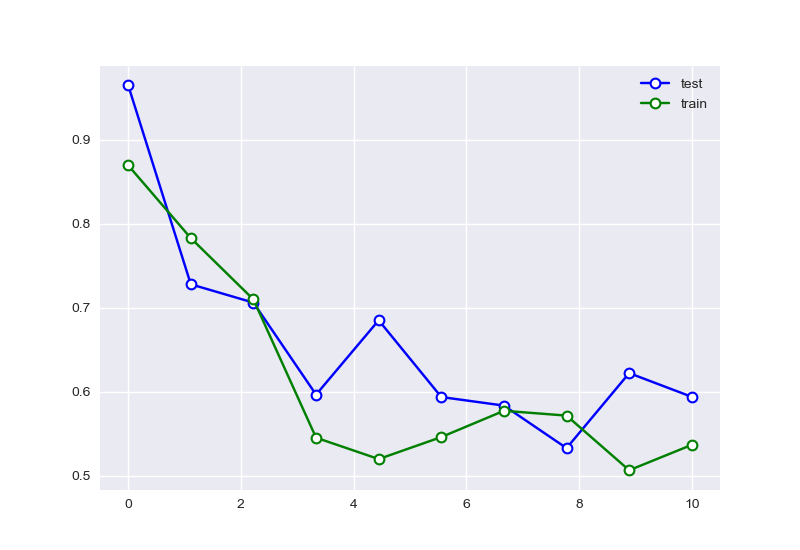
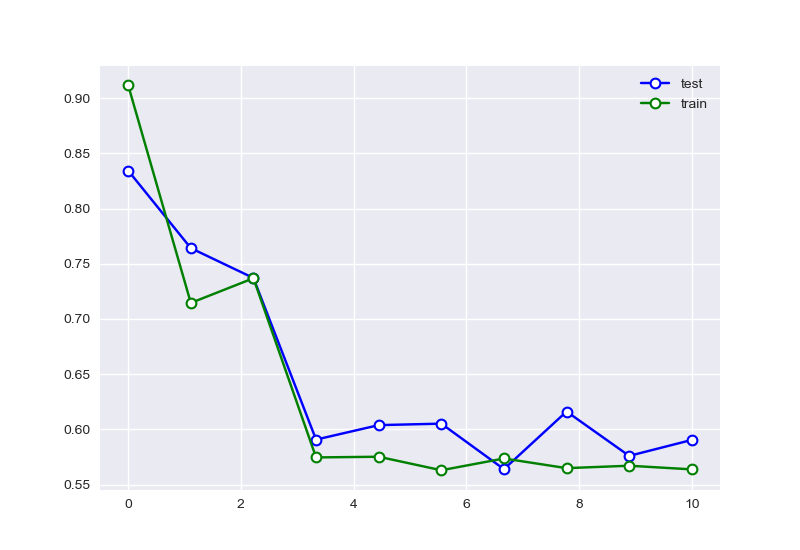
可以看出样本数量增多后，特征的选择有明显的趋势。尝试复现使用样本为10的情况：
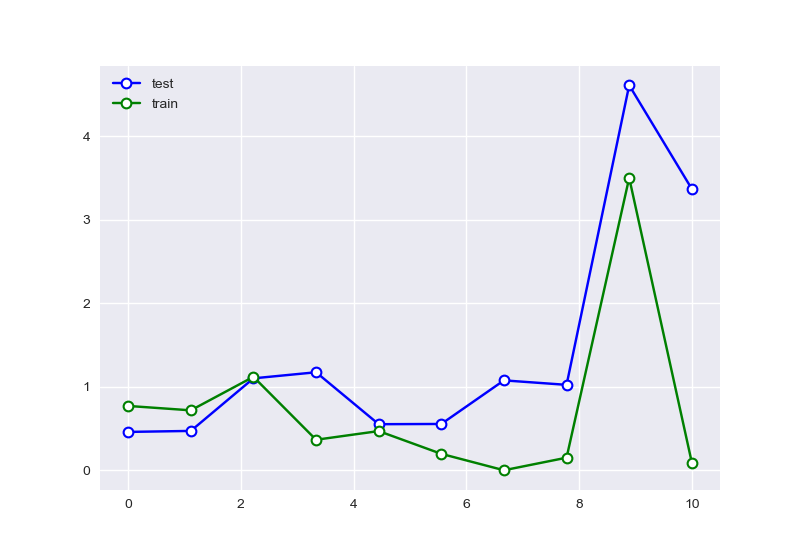且样本数量会明显的影响拟合的效果。
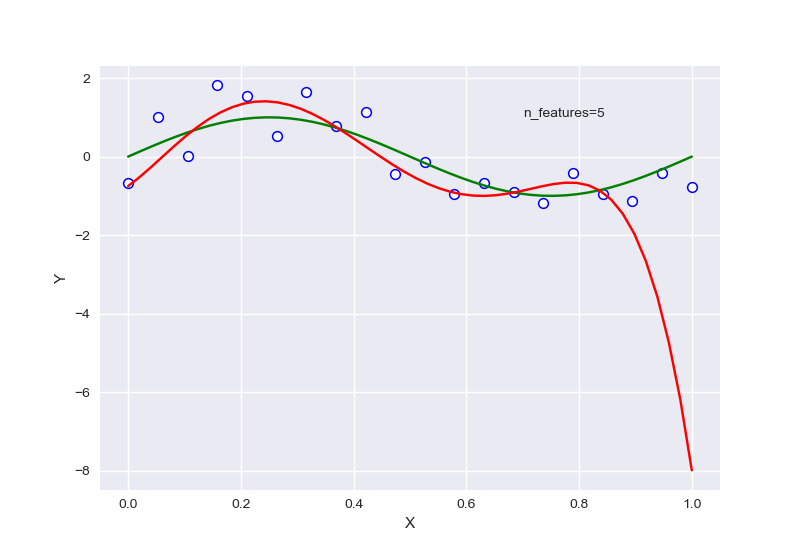
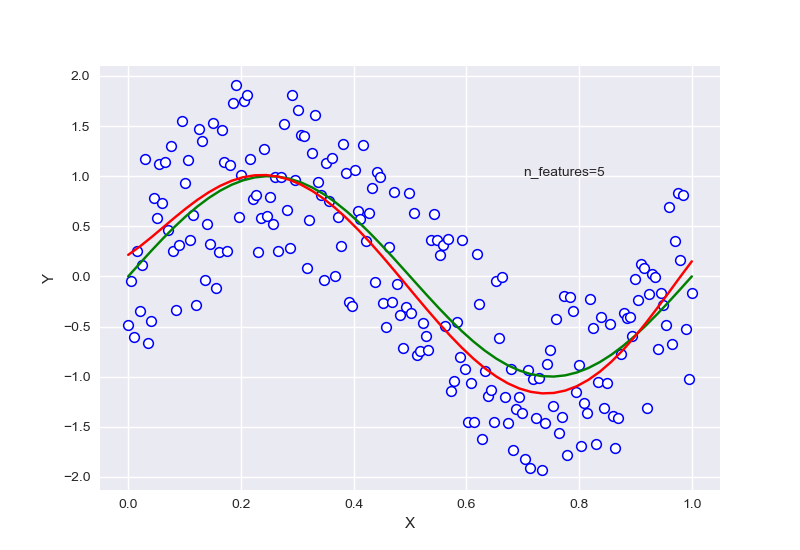
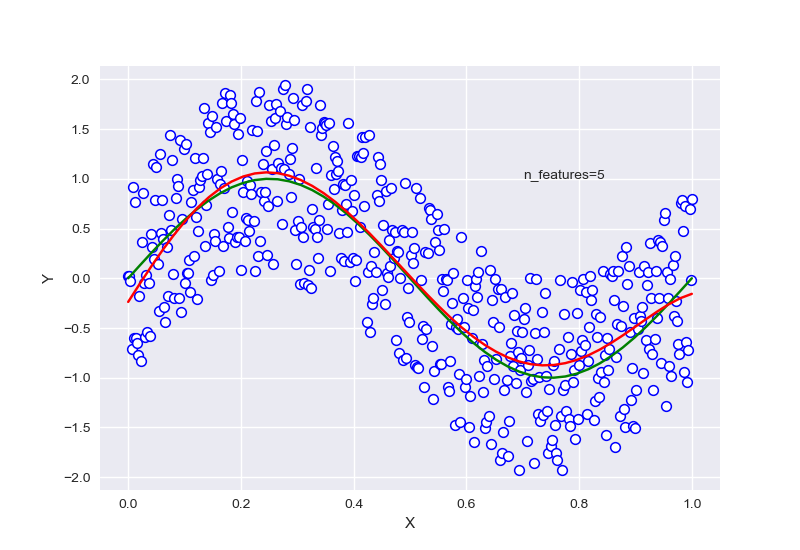
针对样本为10，特征为5的情况下进行正则化：
\(\lambda\)=0.7740859059011267
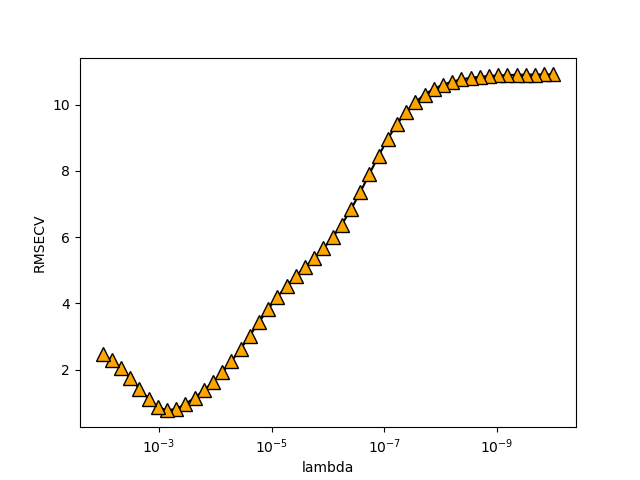
作业二
频率学派与贝叶斯学派
- 频率观点认为频率能够趋近概率，模型的参数是一定的，只要采样数目足够多就能逼近参数值，我的理解是其符合大数定律的思想（此为辛钦大数定律）： \[ \lim_{n\to \infty}P\left(\left|\frac{1}{n}\sum_{i=1}^{n}{a_i-\mu} \right|< \varepsilon\right)=1 \]
- 贝叶斯观点认为模型的参数是在变化的，样本是一定的。 \[ p(w|D)=\frac{p(D|w)p(w)}{p(D)} \] 以一元高斯分布为例，解释样本分布问题：
- 频率： 频率的思想是以样本代替总体，从而得到模型参数，假设有数据集\(D=\{x_1,x_2,\cdot\cdot\cdot,x_n\}\)，则估计得到的一元高斯分布的参数为 \[ \hat\mu=\frac{1}{n}\sum_{i=1}^{n}{x_i} \] \[ \hat{\sigma^2}=\frac{1}{n}\sum_{i=1}^{n}{(x_i-\hat\mu)}^2 \] 样本分布显然是和总体有差异的，对其求期望可以得到，均值为无偏估计，而方差存在偏差，而偏差随着样本数目n的增大而减小（\(E(\hat\sigma^2)=\frac{n-1}{n}\sigma^2\)）。
- 贝叶斯：
贝叶斯的思想认为所有参数都是一个分布，而样本是固定不变的量。所以通过先验尽可能使逼近高斯分布。
\[
p(D|w)=\frac{p(w|D)p(D)}{p(w)}
\] 有似然函数，其中\(p(D)\)为一个常数，可被忽略（归一化），根据课本给出的高斯分布求解结果，发现他的方差和均值均为无偏估计。
## 公式推导
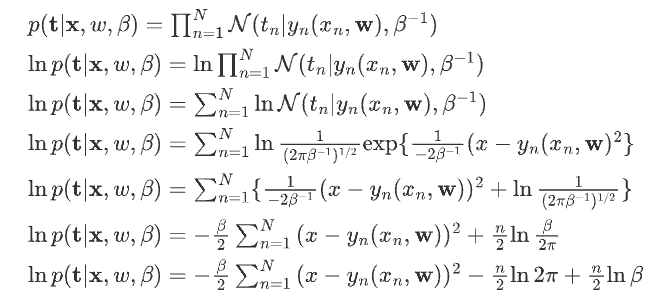
引入先验
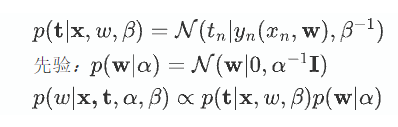
在这里将数据的概率分布进行了归一，认为样本概率为一常数
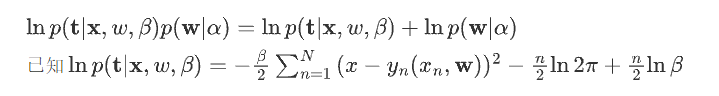
然后对\(\ln p(\mathbf{w}|\alpha)\)求解：
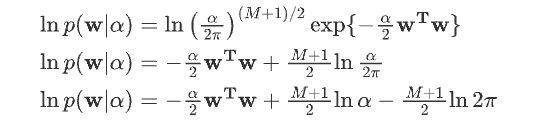
取负数：
\[
-\ln p(\mathbf{t|x},w,\beta)p(\mathbf{w}|\alpha)=
\frac{\beta}{2}\sum_{n=1}^{N}
{(x-y_n(x_n,\mathbf{w}))^2 }
+\frac{\alpha}{2}\mathbf{w^T}\mathbf{w}
-\frac{n}{2}\ln \frac{\beta}{2\pi}-\frac{M+1}{2}\ln \alpha+\frac{M+1}{2}
\ln 2\pi
\] 后三项均为常数，对最大化没有任何影响，因此损失函数为：
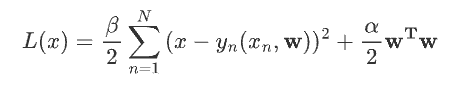
作业三
基函数图像复现
1 | import matplotlib.pyplot as plt |
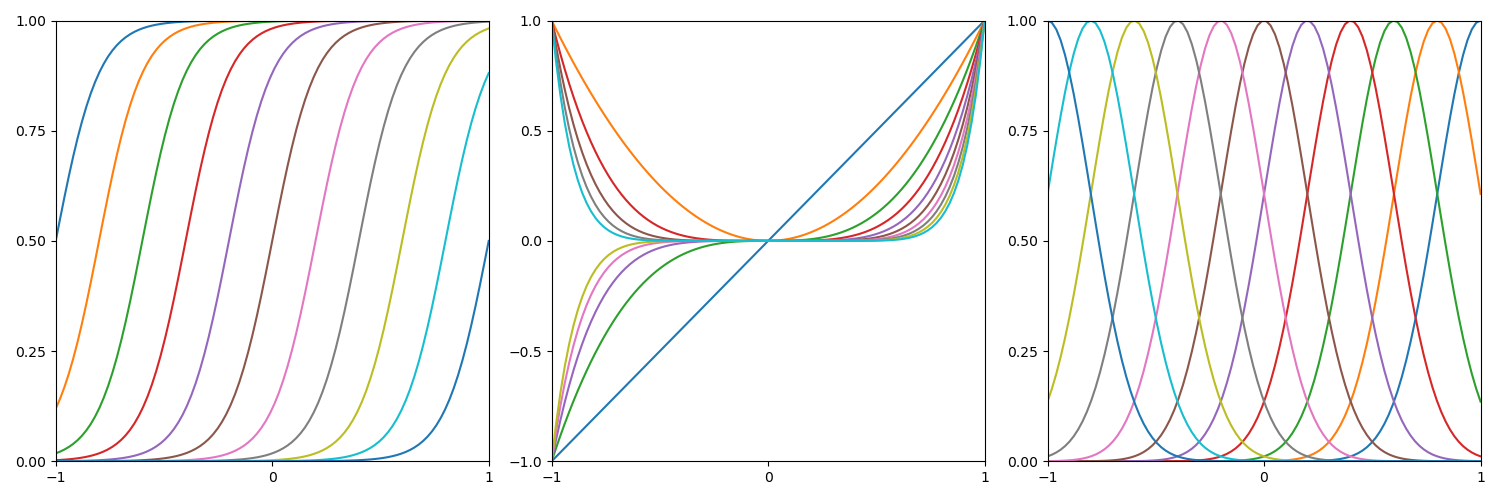
作业四 多项式拟合（加强版）
实验项目结构
/>其中，data储存固化的数据
将数据生成函数与多项式拟合功能分离，建立createData.py
交叉验证函数
线性回归
多项式特征生成和多项式回归
1 | createData.py |
1 | Cross_Validation.py |
1 | linearregression.py |
1 | Polyfeature.py |
1 | PolyRegress.py |
调整\(\beta\)和\(\lambda\)观察RMSE变化
代码如下：
1 | if __name__=='__name__': |
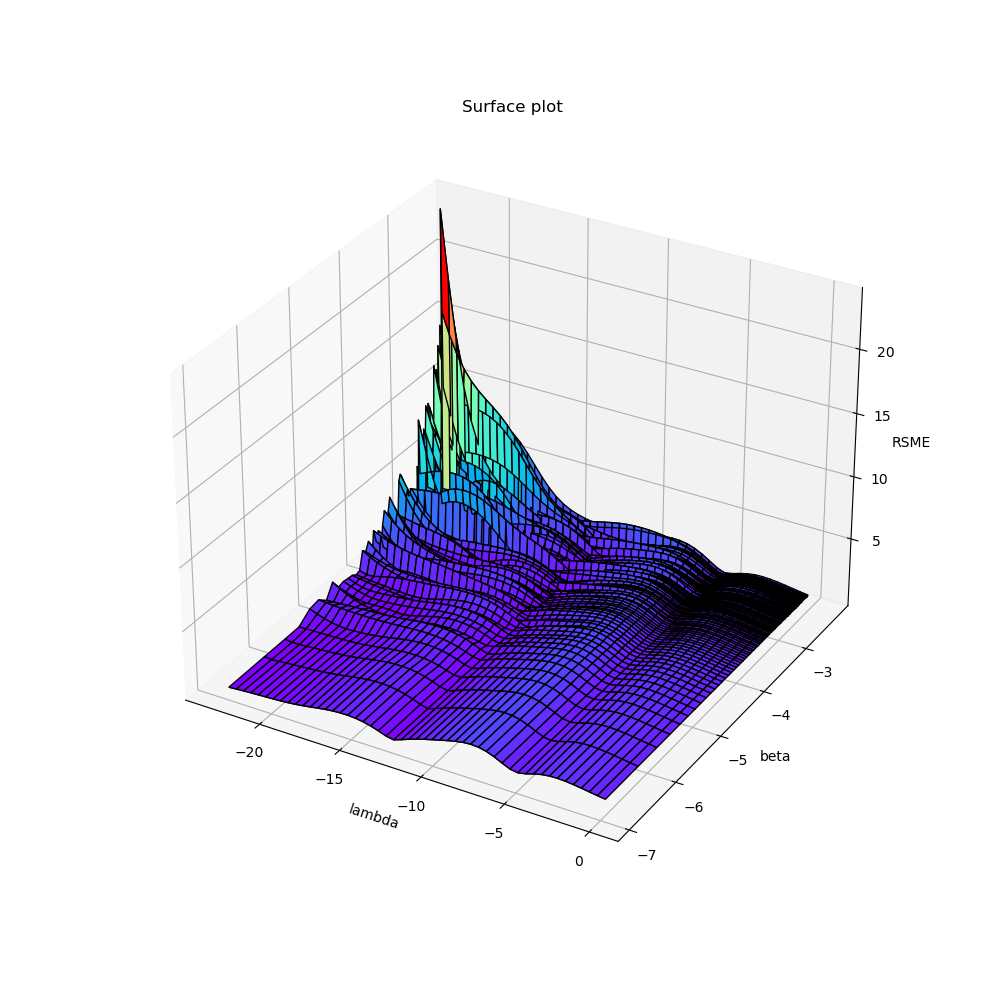
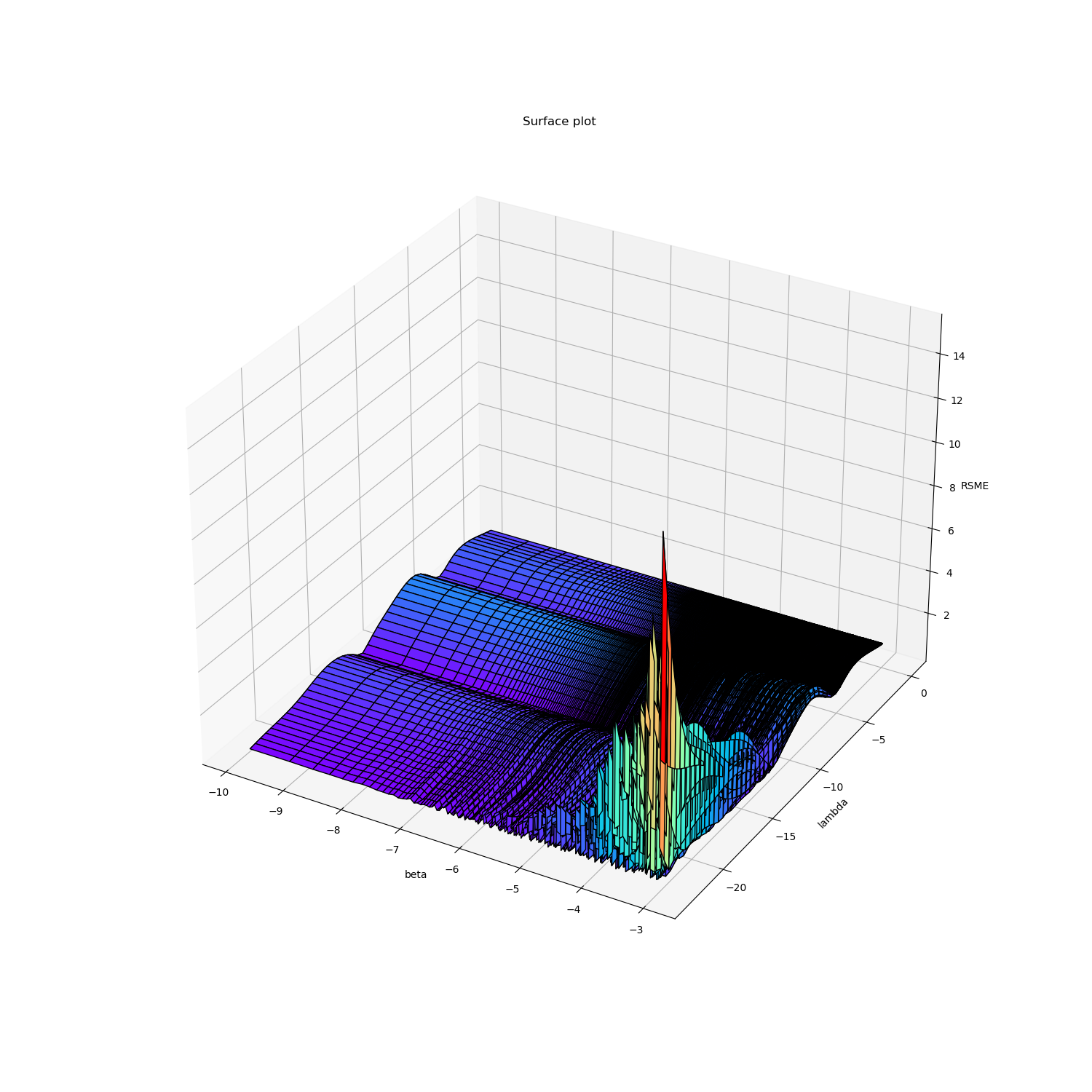
右图\(-\ln \beta\)值作为x轴，\(\ln \lambda\)作为y轴，左图反之。
为了方便观察，对局部作图：
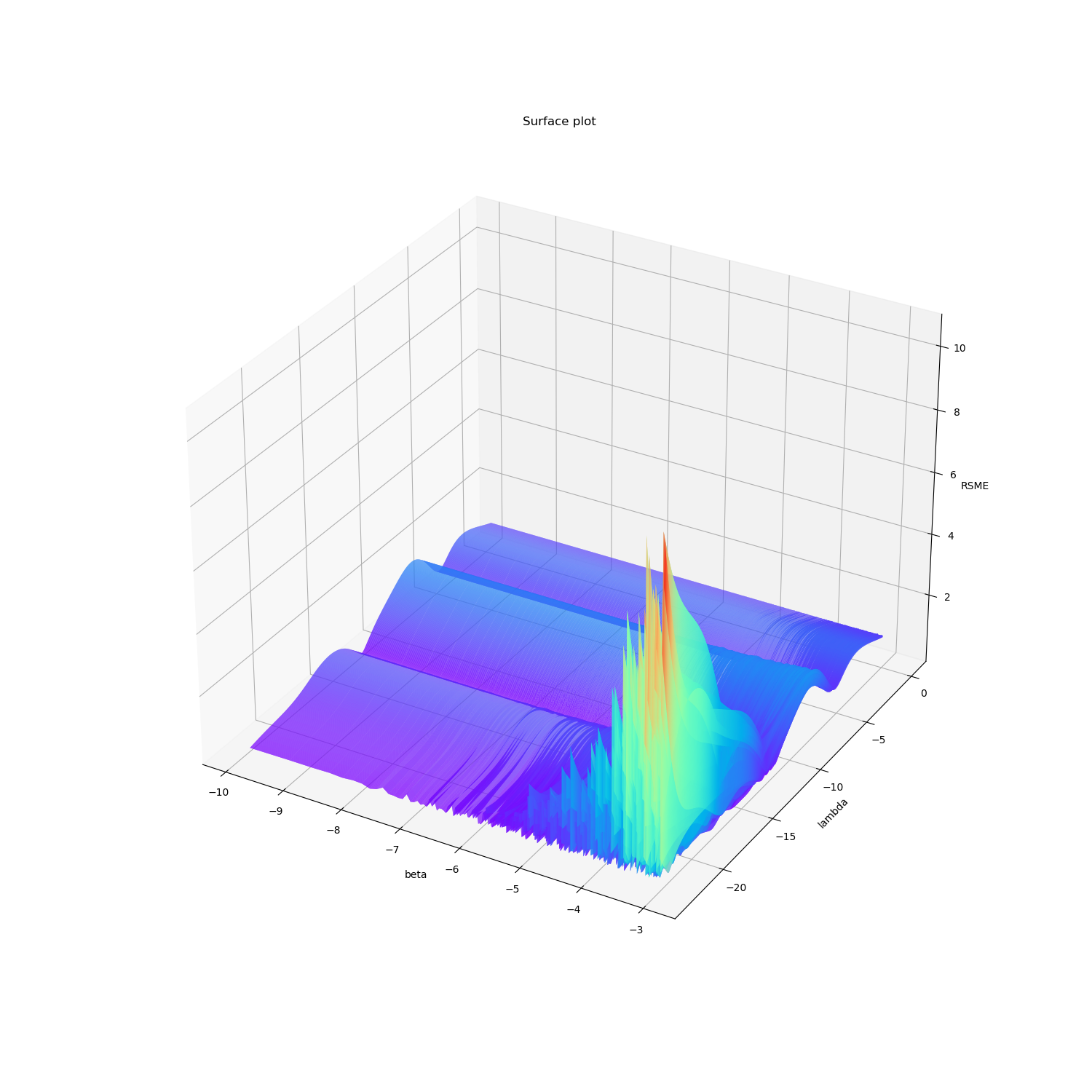
首先，从\(\ln \lambda\)方向观察，可以看出\(\lambda\)对RMSE的影响呈波浪状，存在多个极小值，当\(\lambda\)取很小的值时，在\(-ln\beta\)较大的时候出现了比较严重的过拟合。
然后从\(-\ln \beta\)方向观察，可以看出\(\beta\)对RMSE的影响实际上并不大，呈小而密的波浪趋势。
正则化前后回归系数
代码如下：
1 | # 选择参数lambda，给出拟合表达 |
无正则化：
| \(w\) | 0 | 1 | 2 | 3 | …… | 9 |
|---|---|---|---|---|---|---|
| -0.08673405 | 0.43162238 | 0.5695881 | -0.05816218 | -0.07491257 | ||
| -1.05343403 | -2.17473669 | 11.14510403 | 10.41748047 | |||
| 1.16724815 | -33.31060868 | -34.4765625 | ||||
| 22.29544252 | 56.09375 | |||||
| -60. | ||||||
| -14.375 | ||||||
| 34.796875 | ||||||
| 44.5625 | ||||||
| -2.0625 | ||||||
| -35.390625 |
正则化后：
| \(w\) | 0 | 1 | 2 | 3 | …… | 9 |
|---|---|---|---|---|---|---|
| -0.07776724 | 0.15514244 | 0.17544013 | 0.33805469 | 0.21515437 | ||
| -0.52292037 | -0.38363097 | -0.80726911 | -0.44372143 | |||
| -0.25709792 | -0.42717323 | -0.42050595 | ||||
| 0.41092392 | -0.25649878 | |||||
| -0.10138744 | ||||||
| 0.02127489 | ||||||
| 0.1134249 | ||||||
| 0.1815334 | ||||||
| 0.23170656 | ||||||
| 0.26874031 |
bias-variance结构
程序如下：
1 | # 期望计算 |
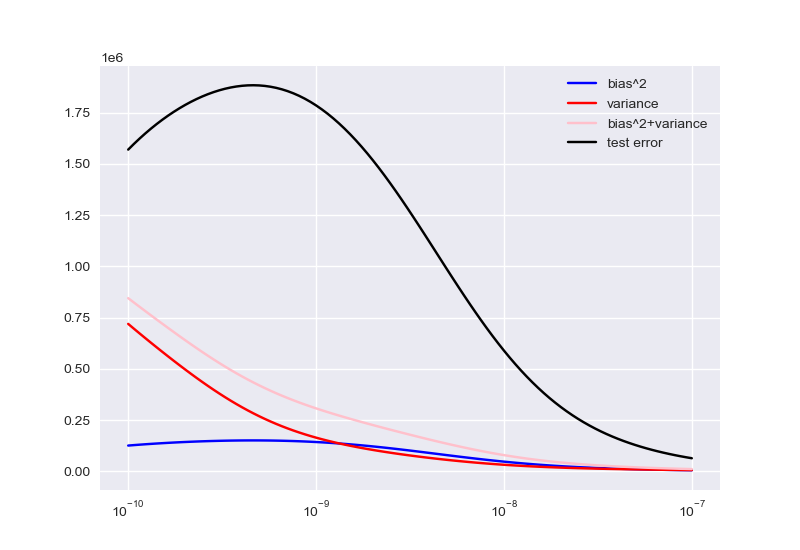
\(degree\)、\(lambda\)寻优过程
1 | rmse_train=[] |
degree寻优：
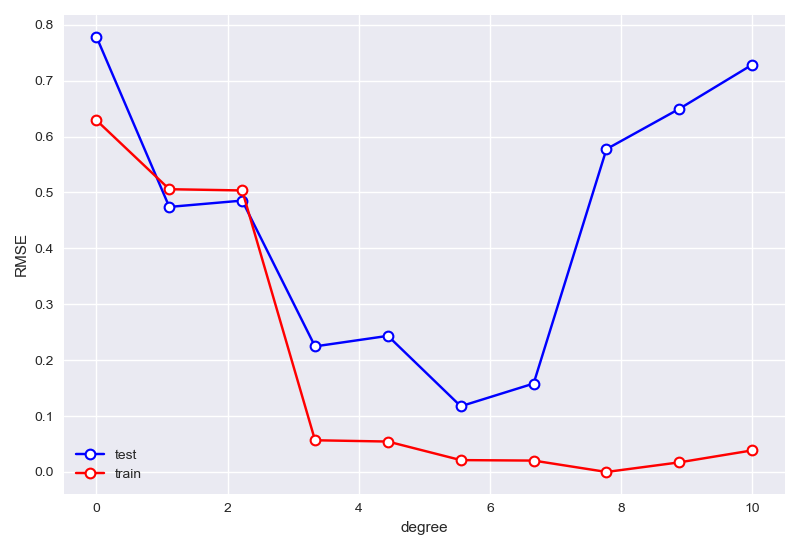
\(lambda\)寻优：
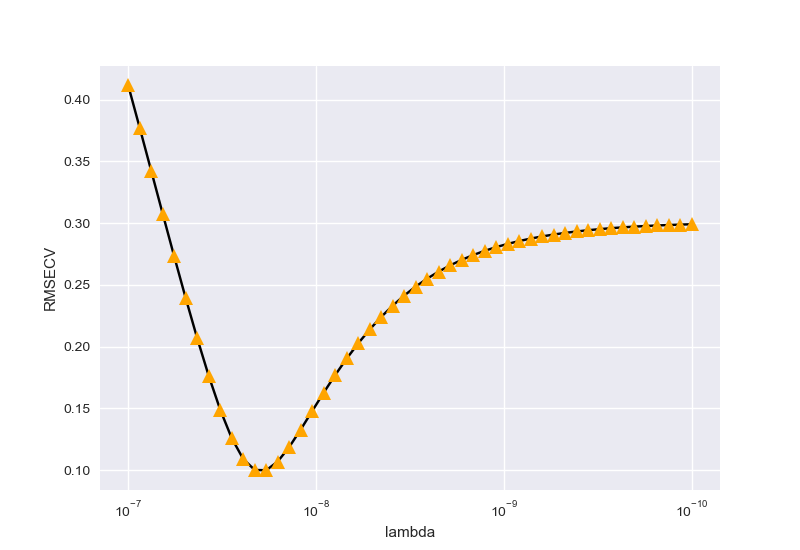
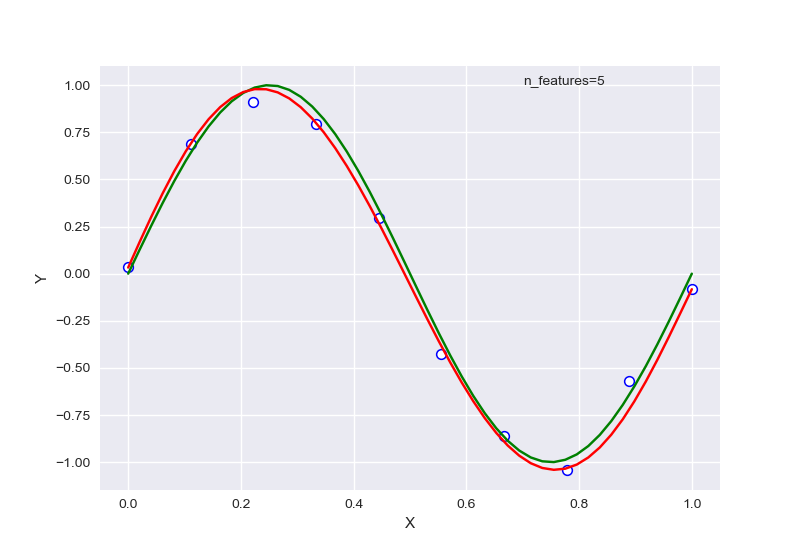
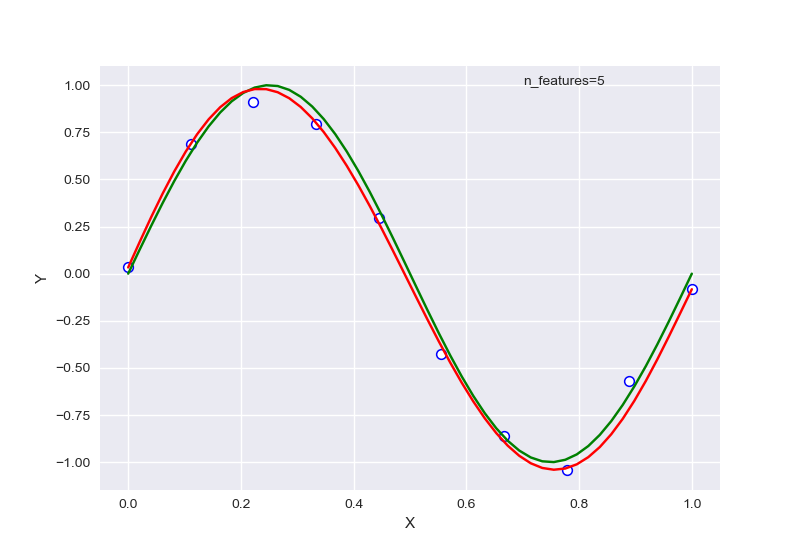
左图为未正则化，右图为正则化后。输出结果为：
1 | best degree is 5 |
样本数目影响
代码如下：
1 | RMSEs=[] |
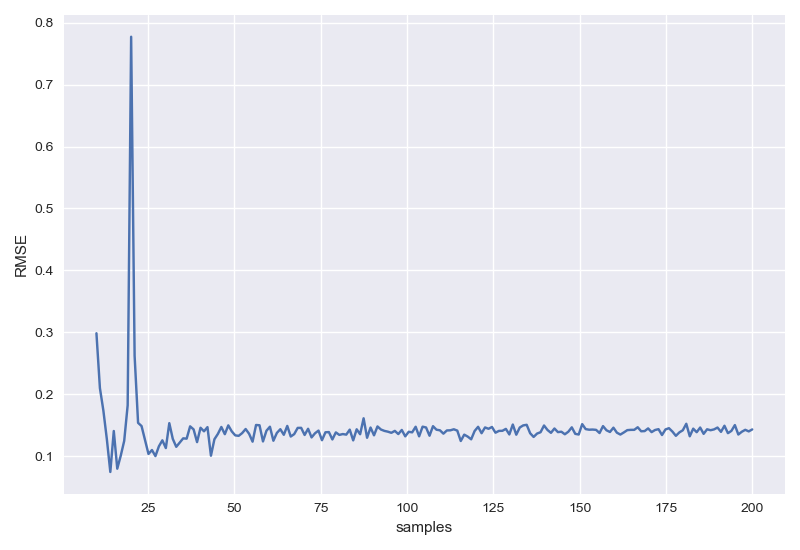
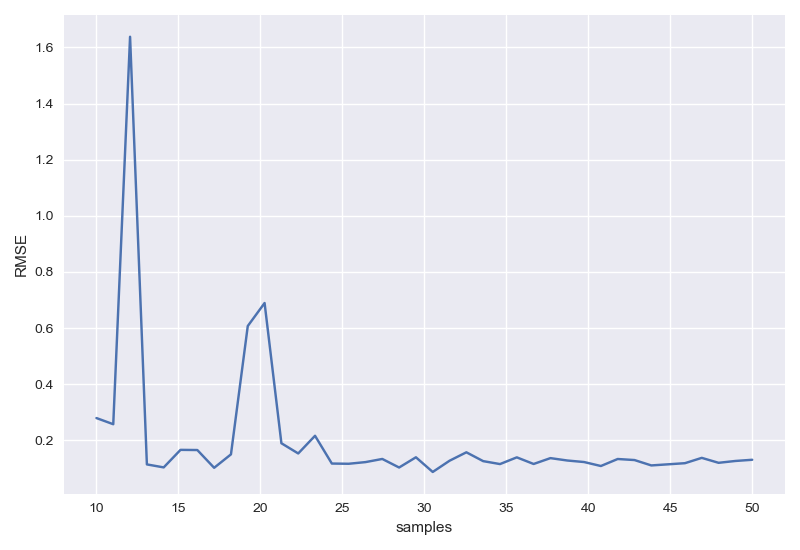
上图是样本数量在（10,200）的RMSE图，下图是样本数量在（10,20）的RMSE图，可以明显看出随着样布数目增长RMSE逐渐趋于稳定，仅有很小的波动。
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 脱碳甲醛的博客！
评论
